Metody numeryczne w RRZ
MATLAB, podobnie jak Mathematica, posiada gotowe narzędzia do rozwiązywania równań zwyczajnych. Wszystkie mają nazwy postaci odeXYZ, gdzie XYZ oznaczają rząd metody, lub inne modyfikacje.
Contents
Wbudowane narzędzia
Chcemy rozwiązać równanie różniczkowe zwyczajne
![$$x' = x + t, \quad x(0) = 0, \quad x\in[0, 2].$$](lab06_eq16228784834062741595.png)
Co musimy zrobić?
- napisać funkcję simpleode[t,x] obliczającą prawą stronę i zapisać ją do pliku simpleode.m,
- uzyć wbudowanej funkcji, by rozwiązać równanie.
function xdot = simpleode(t, x) % Funkcja xdot = simpleode(t, x) oblicza prawą stronę % równania różniczkowego zwyczajnego x' = x + t. xdot = x + t;
Możemy teraz rozwiązać równanie (wykorzystując np. ode23)
tspan = [0, 2]; % przedział czasowy x0 = 0; % warunek początkowy [t, x] = ode45(@simpleode, tspan, x0);
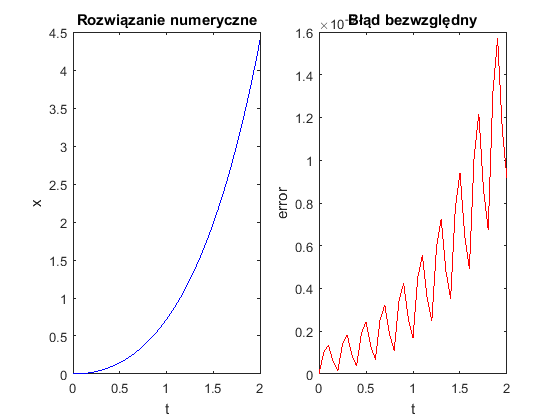
Możemy porównać uzyskany wynik z rozwiązaniem analitycznym.
sol = @(t) exp(t) - t - 1; err = abs(x - sol(t)); figure(1) subplot(1,2,1) plot(t, x, 'b-') xlabel('t') ylabel('x') title('Rozwiązanie numeryczne') subplot(1,2,2) plot(t, err, 'r-') xlabel('t') ylabel('error') title('Błąd bezwzględny')
Własna implementacja
Umiemy już korzystać z wbudowanych narzędzi do rozwiązywania RRZ, czyli funkcji NDSolve[] w Mathematice czy ode23() i ode45() w MATLABie. Zaimplementowane są tam różne metody (np. metoda Eulera, metody Rugego-Kutty) i możemy oczywiście ręcznie zadawać konkretne parametry każdej metody, ale prawdziwą "potęgą" tych narzędzi jest automatyczny dobór metody (lub parametrów metod wybranych przez użytkownika) tak, by osiągnąć najlepszą dokładność kosztem najmniejszej złożoności obliczeniowej problemu.
O co chodzi z metodami numerycznymi?
Spróbujemy zaimplementować cztery metody (z wykładu) i pewną modyfikację, która pozwoli dobierać wartość kroku (siatki) tak by mieć zadaną dokładność.
Będziemy zajmować się rozwiązaniami na pewnym odcinku ![$[0,T]$](lab06_eq02743169367606866090.png) , ale ponieważ rozwiązanie jest numeryczne, to jest zdefiniowane jedynie w punktach siatki, tzn.
, ale ponieważ rozwiązanie jest numeryczne, to jest zdefiniowane jedynie w punktach siatki, tzn.
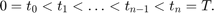
Na początku będziemy rozważać siatkę rónomierną, tzn. 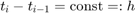 , gdzie
, gdzie 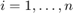 , ale zmodyfikujemy na koniec metody i krok
, ale zmodyfikujemy na koniec metody i krok 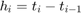 będzie zmienny i dobierany na bieżąco.
będzie zmienny i dobierany na bieżąco.
Przyjmujemy oznaczenie 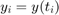 i rozważamy zagadnienie
i rozważamy zagadnienie
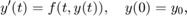
gdzie 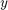 może być także funkcją wektorową (czyli rozważamy układy równań).
może być także funkcją wektorową (czyli rozważamy układy równań).
Metoda Eulera (otwarta)
Podstawową metodę jest wyprowadzona na wykładzie metoda Eulera nazywana czasem otwartą metodą Eulera. Wzór na wartości przybliżenia w kolejnych puntkach siatki jest postaci:
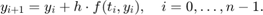
Jest to metoda rzędu 1, rozważamy wersję stałokrokową. Aby ją zaimplementować stworzymy plik m-funkcji EulerMethod.m zawierający następujący kod
function [T,Y] = EulerMethod(odefun, tspan, y0, options)
h = options.h; T = tspan(1):h:tspan(2); Y = zeros(length(y0),length(T));
Y(:,1) = y0; for i = 1:length(T)-1 Y(:,i+1) = Y(:,i) + h*feval(odefun,T(i),Y(:,i)); end
Użyliśmy składni analogicznej do tej, jaka jest zaimplementowana w funkcjach MATLABowych, np. ode23. odefun jest uchwytem do funkcji prawej strony układy równań zapisanej w formie pliku (wtedy należy jako argument funkcji podać @nazwa_pliku) lub w formie funkcji anonimowej (wtedy wystarczy podać nazwę funkcji). Wartości zwracane przez funkcję odefun muszą być zapisane w jednej kolumnie.
Prawa strona równania jest zapisana w pliku TwoBodies.m:
function Rdot = TwoBodies(t, R) % Funkcja Rdot = TwoBodies(t, R) zwraca prawą stronę układu równań % opisującego model dwóch ciał (przy założeniu, że M1+M2=1 oraz G=1). Rdot(1:2) = R(3:4); Rdot(3:4) = -R(1:2)/(norm(R(1:2))^3);
tspan jest wektorem dwuelementowym zawierającym przedział czasowy, w którym rozwiązywane jest równanie, a R0 to warunek początkowy.
tspan = [0 20]; M1 = 0.05; M2 = 1 - M1; R0 = [0.95; 0; 0; 0.6]/M2;
options to struktura zawierająca opcję rozwiązywania układu, np. pole h, które definiuje długość kroku.
h = 1e-2;
options = struct('h', h);
Wówczas możemy rozwiązać zagadnienie i porównać je z rozwiązaniem znalezionym na ostatnich zajęciach w Mathematice.
[T,R] = EulerMethod(@TwoBodies, tspan, R0, options); R1_Euler = M2*R(1:2,:); R2_Euler = -M1*R(1:2,:); load('trajektorie.mat'); figure(2) subplot(2,2,1) plot(T,R1_Euler(1,:),'b.',R1(:,1),R1(:,2),'r-') xlabel('t') ylabel('R1x') legend('metoda Eulera','rozwiazanie') subplot(2,2,2) plot(T,R1_Euler(2,:),'b.',R1(:,1),R1(:,3),'r-') xlabel('t') ylabel('R1y') legend('metoda Eulera','rozwiazanie') subplot(2,2,3) plot(T,R2_Euler(1,:),'b.',R2(:,1),R2(:,2),'r-') xlabel('t') ylabel('R2x') legend('metoda Eulera','rozwiazanie') subplot(2,2,4) plot(T,R2_Euler(2,:),'b.',R2(:,1),R2(:,3),'r-') xlabel('t') ylabel('R2y') legend('metoda Eulera','rozwiazanie')
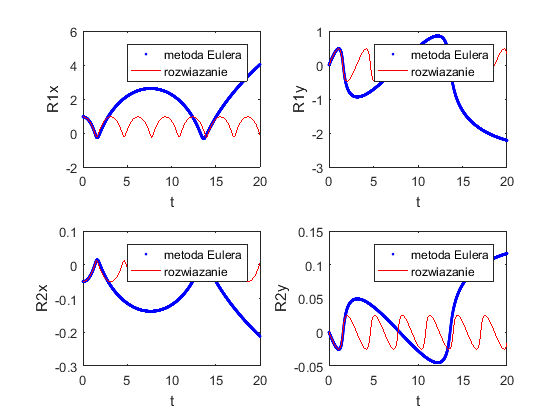
Zmniejszając długość kroku można zaobserwować, że błąd się zmniejsza (ale metoda nie jest specjalnie dobra)
Metoda Rungego-Kutty rzędu 4
Zaimplementujemy jedną z metod Rungego-Kutty, rzędu 4. Ogólnie metody RK mają postać
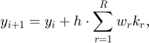
gdzie w przypadku metody RK4 mamy 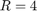 i parametry mają postać
i parametry mają postać
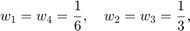
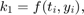
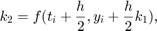
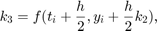
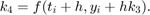
Implementacja metody w pliku RK4Method.m jest postaci:
function [T,Y] = RK4Method(odefun, tspan, y0, options)
h = options.h; T = tspan(1):h:tspan(2); Y = zeros(length(y0),length(T));
Y(:,1) = y0; w1 = 1/6; w2 = 1/3; w3 = 1/3; w4 = 1/6; for i = 1:length(T)-1 k1 = feval(odefun,T(i),Y(:,i)); k2 = feval(odefun,T(i)+h/2, Y(:,i)+h/2*k1); k3 = feval(odefun,T(i)+h/2, Y(:,i)+h/2*k2); k4 = feval(odefun,T(i)+h, Y(:,i)+h*k3); Y(:,i+1) = Y(:,i) + h*(w1*k1+w2*k2+w3*k3+w4*k4); end
Przetestujmy metodę tak samo jak wcześniej.
[T,R] = RK4Method(@TwoBodies, tspan, R0, options); R1_RK4 = M2*R(1:2,:); R2_RK4 = -M1*R(1:2,:); figure(3) subplot(2,2,1) plot(T,R1_RK4(1,:),'b.',R1(:,1),R1(:,2),'r-') xlabel('t') ylabel('R1x') legend('metoda RK4','rozwiazanie') subplot(2,2,2) plot(T,R1_RK4(2,:),'b.',R1(:,1),R1(:,3),'r-') xlabel('t') ylabel('R1y') legend('metoda RK4','rozwiazanie') subplot(2,2,3) plot(T,R2_RK4(1,:),'b.',R2(:,1),R2(:,2),'r-') xlabel('t') ylabel('R2x') legend('metoda RK4','rozwiazanie') subplot(2,2,4) plot(T,R2_RK4(2,:),'b.',R2(:,1),R2(:,3),'r-') xlabel('t') ylabel('R2y') legend('metoda RK4','rozwiazanie')
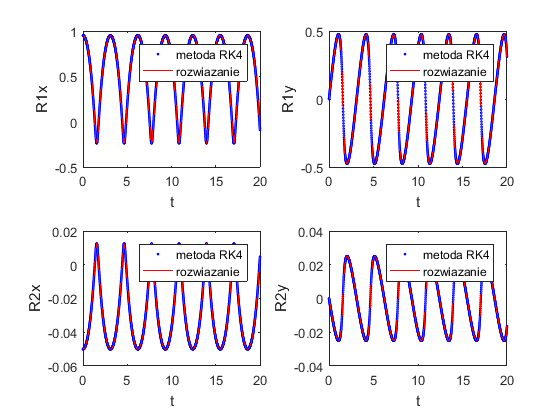
Co i jak poprawić?
Metody ze stałym krokiem potrafią być szybko-zbieżne, ale już nawet w powyższych przykładach widać, że przy zbyt małym roku błąd potrafi rosnąć do bardzo dużych wartości (zazwyczaj wtedy, gdy pochodna robi się zbyt duża). Dlaczego więc rozwiązywać wszędzie z tak samo dużym krokiem? Błąd można zmniejszyć, jeśli będziemy dynamicznie dobierać wielkość kroku. Z drugiej strony, jeśli rozwiązanie jest mniej zmienne, to błędy będą niższe i można wtedy wielkość kroku zwiększać.
Zacznijmy od przypomnienia pojęcia lokalnego błędu. Dla schematu
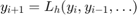
błędem lokalnym nazywamy wielkość
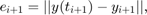
gdzie 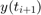 to prawdziwa wartość rozwiązania w danym punkcie, przy założeniu, że wartości
to prawdziwa wartość rozwiązania w danym punkcie, przy założeniu, że wartości 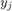 jest dokładne dla
jest dokładne dla 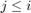 . Mówimy, że metoda jest rzędu
. Mówimy, że metoda jest rzędu 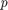 , jeśli
, jeśli
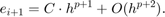
Jak dynamicznie dobierać wartość kroku 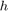 ? Chcemy, żeby błąd lokalny był maksymalnie
? Chcemy, żeby błąd lokalny był maksymalnie 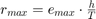 , gdzie
, gdzie 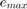 jest zadaną dokładnością. Stosuje się tutaj tzw. zasadę Rungego: wartości w kolejnym punkcie siatki liczymi na dwa sposoby:
jest zadaną dokładnością. Stosuje się tutaj tzw. zasadę Rungego: wartości w kolejnym punkcie siatki liczymi na dwa sposoby:
- stosując formułę z krokiem
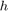 - dostajemy
- dostajemy 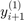 (standardowe rozwiązanie);
(standardowe rozwiązanie); - dwukrotnie stosujemy formułę z krokiem
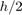 - dostajemy
- dostajemy 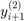 .
.
Zauważmy, że
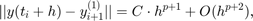
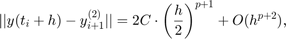
i wielkość
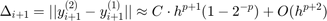
posłuży do oszacowania lokalnego błędu. Błąd przy obliczaniu 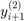 jest równy (po pominięciu składników odpowiednio niskiego rzędu)
jest równy (po pominięciu składników odpowiednio niskiego rzędu)
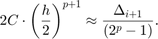
Obliczmy teraz takie 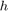 , dla którego spełnione będą wymagania dokładności:
, dla którego spełnione będą wymagania dokładności:
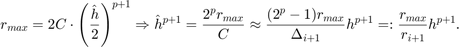
Algorytm korekcji kroku jest następujący:
- mamy policzone
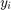 i dany krok
i dany krok 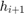 ,
, - liczymy
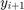 dwiema metodami i obliczamy
dwiema metodami i obliczamy 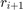 oraz
oraz 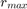 ,
, - jeśli
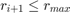 to
to 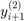 jest wystarczająco dokładne i kontynuujemy z krokiem
jest wystarczająco dokładne i kontynuujemy z krokiem 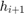 , jeśli
, jeśli 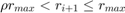 lub
lub
![$$h_{i+1} = \frac{h_{i+1}}{\max\left\{\frac{1}{10},
\sqrt[p+1]{\frac{r_{i+1}}{r_{max}}}\right\}},$$](lab06_eq03934467985515926366.png)
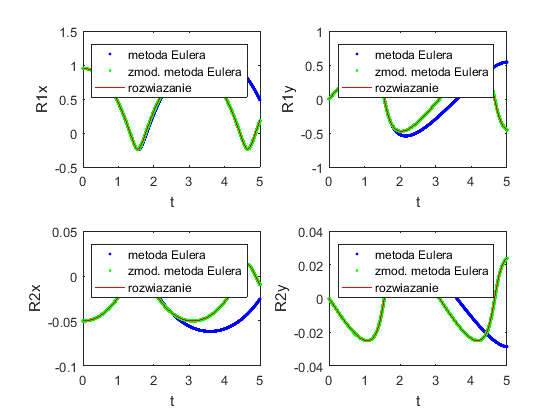
jeśli 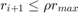 ,
,
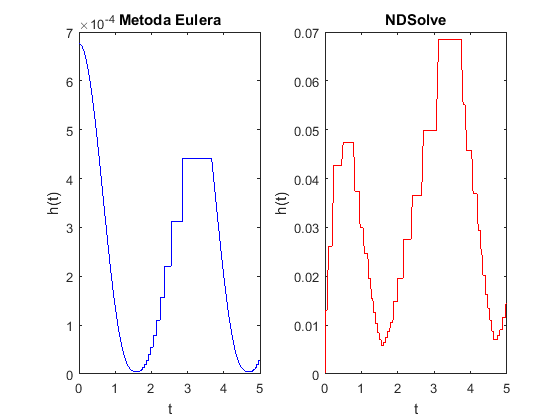
- jeśli nie, to powtarzamy liczenie
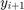 dla nowego kroku
dla nowego kroku
![$$\hat{h}_{i+1} = \frac{h_{i+1}}{\min\left\{10,
\sqrt[p+1]{\frac{r_{i+1}}{r_{max}}}\right\}}.$$](lab06_eq02602095580041037346.png)
Kod zawarty w pliku EulerModMethod.m modyfikuje w ten sposób metodę Eulera (metodę 1-go rzędu):
function [T,Y] = EulerModMethod(odefun, tspan, y0, options)
h = options.h; e = options.emax; rho = options.rho;
T = tspan(1); Y = y0;
while T(end) <= tspan(2) % obliczamy y_{i+1} dwiema metodami y1 = Y(:,end) + h*feval(odefun,T(end),Y(:,end)); y2 = Y(:,end) + h/2*feval(odefun,T(end),Y(:,end)); y2 = y2 + h/2*feval(odefun,T(end)+h/2,y2); % obliczamy blad obciecia (metoda rzedu 1) r = norm(y2 - y1); rmax = h*e/(tspan(2)-tspan(1)); % czy modyfikujemy krok? if r <= rmax T = [T, T(end)+h]; Y = [Y, y2]; if r <= rho*rmax h = h/max(0.1, sqrt(r/rmax)); end else h = h/min(10, sqrt(r/rmax)); end end
Przetestujmy metodę i porównajmy z klasyczną metodą Eulera.
tspan = [0 5]; options = struct('h',0.002,'emax',0.001,'rho',0.5); [Ta,Ra] = EulerMethod(@TwoBodies, tspan, R0, options); R1_EulerA = M2*Ra(1:2,:); R2_EulerA = -M1*Ra(1:2,:); [Tb,Rb] = EulerModMethod(@TwoBodies, tspan, R0, options); R1_EulerB = M2*Rb(1:2,:); R2_EulerB = -M1*Rb(1:2,:); figure(4) subplot(2,2,1) plot(Ta,R1_EulerA(1,:),'b.',Tb,R1_EulerB(1,:),'g.',R1(:,1),R1(:,2),'r-') xlim(tspan) xlabel('t') ylabel('R1x') legend('metoda Eulera','zmod. metoda Eulera','rozwiazanie') subplot(2,2,2) plot(Ta,R1_EulerA(2,:),'b.',Tb,R1_EulerB(2,:),'g.',R1(:,1),R1(:,3),'r-') xlim(tspan) xlabel('t') ylabel('R1y') legend('metoda Eulera','zmod. metoda Eulera','rozwiazanie') subplot(2,2,3) plot(Ta,R2_EulerA(1,:),'b.',Tb,R2_EulerB(1,:),'g.',R2(:,1),R2(:,2),'r-') xlim(tspan) xlabel('t') ylabel('R2x') legend('metoda Eulera','zmod. metoda Eulera','rozwiazanie') subplot(2,2,4) plot(Ta,R2_EulerA(2,:),'b.',Tb,R2_EulerB(2,:),'g.',R2(:,1),R2(:,3),'r-') xlim(tspan) xlabel('t') ylabel('R2y') legend('metoda Eulera','zmod. metoda Eulera','rozwiazanie')
Widać przy okazji koszt poniesiony w liczbie wykonanych kroków.
disp([length(Ta),length(Tb)]) figure(5) subplot(1,2,1) plot(Tb(2:end),Tb(2:end)-Tb(1:end-1),'b') xlim(tspan) xlabel('t') ylabel('h(t)') title('Metoda Eulera') subplot(1,2,2) plot(R1(2:end,1),R1(2:end,1)-R1(1:end-1,1),'r') xlim(tspan) xlabel('t') ylabel('h(t)') title('NDSolve')
2501 172231
Uzupełnienie problemu
Zmodyfikujmy teraz nasz problem, dodając do niego trzecie ciało.
tspan = [0 5]; M1 = 0.05; M2 = 1 - M1; R0(1:4,1) = [0.95; 0; 0; 0.6]/M2; R0(5:8,1) = [0.98; 0; 0.134; -0.2]; h = 1e-3; options = struct('h', h); [T,R] = RK4Method(@ThreeBodies, tspan, R0, options); R1_RK4 = M2*R(1:2,:); R2_RK4 = -M1*R(1:2,:); R3_RK4 = R(5:6,:); figure(6) subplot(3,2,1) plot(T,R1_RK4(1,:),'b.',R1(:,1),R1(:,2),'r-') xlim(tspan) xlabel('t') ylabel('R1x') legend('metoda RK4','rozwiazanie') subplot(3,2,2) plot(T,R1_RK4(2,:),'b.',R1(:,1),R1(:,3),'r-') xlim(tspan) xlabel('t') ylabel('R1y') legend('metoda RK4','rozwiazanie') subplot(3,2,3) plot(T,R2_RK4(1,:),'b.',R2(:,1),R2(:,2),'r-') xlim(tspan) xlabel('t') ylabel('R2x') legend('metoda RK4','rozwiazanie') subplot(3,2,4) plot(T,R2_RK4(2,:),'b.',R2(:,1),R2(:,3),'r-') xlim(tspan) xlabel('t') ylabel('R2y') legend('metoda RK4','rozwiazanie') subplot(3,2,5) plot(T,R3_RK4(1,:),'b.',R3(:,1),R3(:,2),'r-') xlim(tspan) xlabel('t') ylabel('R3x') legend('metoda RK4','rozwiazanie') subplot(3,2,6) plot(T,R3_RK4(2,:),'b.',R3(:,1),R3(:,3),'r-') xlim(tspan) xlabel('t') ylabel('R3y') legend('metoda RK4','rozwiazanie')
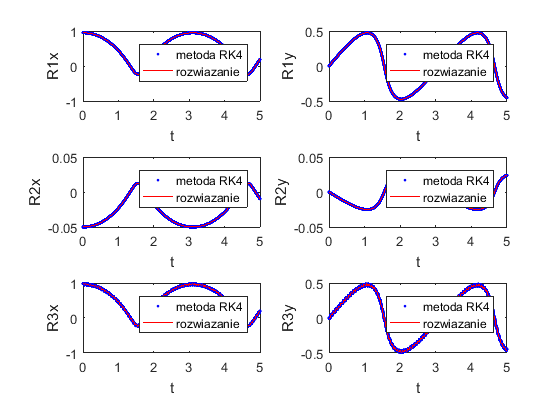
Zauważmy, że nawet metoda Runge-Kutty nie jest w stanie poradzić sobie z szybkimi zmianami, jakie zachodzą w rozwiązaniu R3.