Równania cząstkowe w MATLABie
Contents
Schematy różnicowe dla równania transportu
Rozwiązywanie numeryczne równań cząstkowych rozpoczniemy od prostego przykładu równania transportu, tzn.
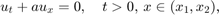
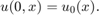
Zauważmy, że musimy zadać jeszcze warunek brzegowy. Jednak to, który warunek brzegowy zadamy (by problem był dobrze określony) jest ściśle związane z samym równaniem: jeśli 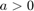 , to musimy zadać warunek dla
, to musimy zadać warunek dla 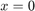 , jeśli
, jeśli 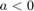 , to dla
, to dla 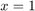 .
.
Przyjmiemy oznaczenie 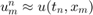 , gdzie
, gdzie 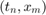 to punkty na siatce (
to punkty na siatce (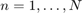 ,
, 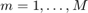 ). Stwórzmy funkcję NumericSolve, która dla zadanych parametrów równania będzie je rozwiązywała każdym z poniższych schematów:
). Stwórzmy funkcję NumericSolve, która dla zadanych parametrów równania będzie je rozwiązywała każdym z poniższych schematów:
- schemat forward-time forward-space:
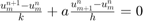 ,
, - schemat forward-time backward-space:
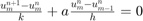 ,
, - schemat forward-time central-space:
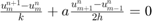 .
.
Zauważmy, że musimy pamiętać nie tylko o zaimplementowaniu warunku początkowego i brzegowego, ale także musimy uzupełnić (czasami) wartości na drugim brzegu. Tam, gdzie będziemy potrzebować tzw. numerycznego warunku brzegowego, użyjemy wartości odległej o 1 na siatce (czyli np. 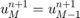 ).
).
Implementacja NumericSolve
function [u, X, T, M, N] = NumericSolve(a, u0, ht, t, x, lambda, h, method) % Równanie u_t + a*u_x = 0 z warunkiem początkowym u0 i warunkiem brzegowym % ht. Dla a>0, ht znajduje się na lewym brzegu, a dla a<0 na prawym. % t=[t0, t1] - przedział czasowy % x=[x0, x1] - przedział przestrzenny % h - krok przestrzenny, lambda = h/k, gdzie k - krok czasowy % Metody: % (1) forward-time forward-space % (2) forward-time backward-space % (3) forward-time central-space
k = lambda*h;
X = x(1):h:x(2); T = t(1):k:t(2); M = length(X); N = length(T);
u = zeros(M,N);
% uzupełnienie warunku początkowego: for i=1:M, u(i,1) = feval(u0,X(i)); end
% uzupełnienie warunku brzegowego: if a>0 for i=2:N, u(1,i) = feval(ht,T(i)); end else for i=2:N, u(M,i) = feval(ht,T(i)); end end
if strcmp(method,'forward-time forward-space') for n=2:N for m=2:(M-1) u(m,n) = u(m,n-1) - a*lambda*( u(m+1,n-1) - u(m,n-1) ); end
% uzupełnienie brzegowego warunku numerycznego
if a>0
u(M,n) = u(M-1,n);
else
u(1,n) = u(1,n-1) - a*lambda*( u(2,n-1) - u(1,n-1) );
end
endelseif strcmp(method,'forward-time backward-space') for n=2:N for m=2:(M-1) u(m,n) = u(m,n-1) - a*lambda*( u(m,n-1) - u(m-1,n-1) ); end
% uzupełnienie brzegowego warunku numerycznego
if a>0
u(M,n) = u(M,n-1) - a*lambda*( u(M,n-1) - u(M-1,n-1) );
else
u(1,n) = u(1+1,n);
end
endelseif strcmp(method,'forward-time central-space') for n=2:N for m=2:(M-1) u(m,n) = u(m,n-1) - a*lambda*( u(m+1,n-1) - u(m-1,n-1) )/2; end
% uzupełnienie brzegowego warunku numerycznego
if a>0
u(M,n) = u(M-1,n);
else
u(1,n) = u(1+1,n);
end
endend
Przetestowanie działania zaimplementowanych metod
Zajmijmy się na początek przykładem
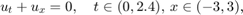
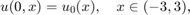
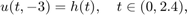
gdzie 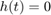 oraz
oraz
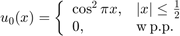
i przetestujmy działanie każdego schematu dla 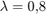 oraz
oraz 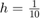 ,
, 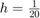 ,
, 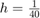 .
.
a = 1; u0 = @(x) (abs(x)<=0.5).*(cos(pi*x)).^2; ht = @(t) 0; x = [-3,3]; t = [0,2.4]; h1 = 1/10; h2 = 1/20; h3 = 1/40; lambda = 0.8; method1 = 'forward-time forward-space'; method2 = 'forward-time backward-space'; method3 = 'forward-time central-space'; h = h3; [u1, X, T, M, N] = NumericSolve(a, u0, ht, t, x, lambda, h, method1); [u2] = NumericSolve(a, u0, ht, t, x, lambda, h, method2); [u3] = NumericSolve(a, u0, ht, t, x, lambda, h, method3); % for n = 1:N n = 20; plot(X,u1(:,n),'g') hold on; plot(X,u2(:,n),'b') plot(X,u3(:,n),'c') plot(X,u0((X)-a*T(n)),'-r') hold off; ylim([-0.1,1.6]) legend(method1,method2,method3,'real solution') xlabel('x'); ylabel('u(t,x)'); title(['time: ',num2str(T(n),'%.2f'),'s']) pause(0.2) % end
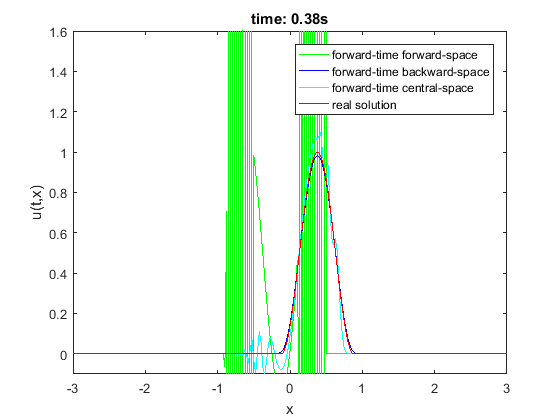
Zauważmy, że tylko metoda forward-time backward-space daje rozsądne wyniki. Spróbujmy zmodyfikować zagadnienie (niech 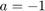 , wtedy warunek brzegowy zadany jest na drugim brzegu). Role schematów się odwracają - tym razem tylko metoda forward-time forward-space daje wyniki zbliżone do prawdziwych. Jest to związane z faktem, że dla
, wtedy warunek brzegowy zadany jest na drugim brzegu). Role schematów się odwracają - tym razem tylko metoda forward-time forward-space daje wyniki zbliżone do prawdziwych. Jest to związane z faktem, że dla 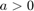 metoda forward- time backward-space jest zbieżna, a dla
metoda forward- time backward-space jest zbieżna, a dla 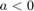 nie (i analogicznie dla drugiego schematu). Widzimy też, że zmniejszenie kroku
nie (i analogicznie dla drugiego schematu). Widzimy też, że zmniejszenie kroku  znacząco poprawia własności schematów.
znacząco poprawia własności schematów.
Stabilność metod
Wiemy, że dla 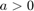 metoda forward-time backward-space jest zbieżna, ponadto z wykładu wiemy, że jest zgodna z równaniem (dla dowolnego
metoda forward-time backward-space jest zbieżna, ponadto z wykładu wiemy, że jest zgodna z równaniem (dla dowolnego  ). Zbadajmy teraz stabilność tej metody. Wiemy (również z wykładu), że schemat jest stabilny, jeśli
). Zbadajmy teraz stabilność tej metody. Wiemy (również z wykładu), że schemat jest stabilny, jeśli 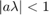 . Potwierdźmy ten fakt doświadczalnie.
. Potwierdźmy ten fakt doświadczalnie.
h = 1/10; lambda1 = 0.8; lambda2 = 1.6; method = 'forward-time backward-space'; [u4, X, T1, M, N1] = NumericSolve(a, u0, ht, t, x, lambda1, h, method); [u5, X, T2, M, N2] = NumericSolve(a, u0, ht, t, x, lambda2, h, method); % for n = 1:N2 n = 10; n2 = find(T1==T2(n)); plot(X,u4(:,n2),'b') hold on; plot(X,u5(:,n),'g') plot(X,u0((X)-a*T2(n)),'-r') hold off; ylim([-0.1,1.6]) legend('stable','unstable','real solution') xlabel('x'); ylabel('u(t,x)'); title(['time: ',num2str(T(n),'%.2f'),'s']) pause(0.2) % end
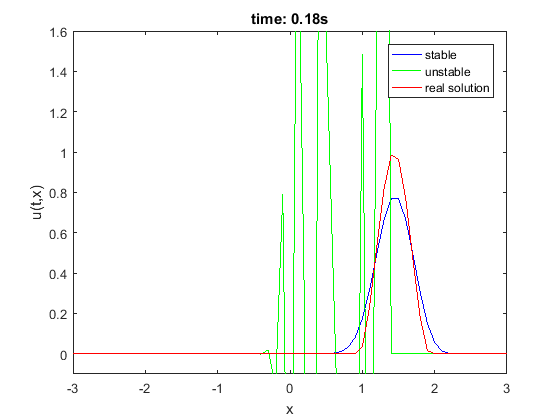
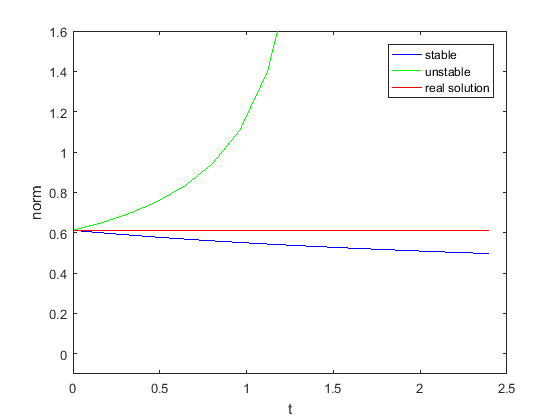
Warto sprawdzić przy tym, jak zmienia się norma L2 rozwiązania (w przypadku schematu niestabilnego powinna rosnąć nieograniczenie).
stability1 = zeros(size(T1)); stability2 = zeros(size(T2)); stability0 = sqrt(h)*norm(u0(X))*ones(size(t)); for n = 1:N1 stability1(n) = sqrt(h)*norm(u4(:,n)); end for n = 1:N2 stability2(n) = sqrt(h)*norm(u5(:,n)); end plot(T1,stability1,'b',T2,stability2,'g',t,stability0,'-r') ylim([-0.1,1.6]) legend('stable','unstable','real solution') xlabel('t'); ylabel('norm');
Podsumowanie
Przedstawione metody są zaledwie podstawowymi metodami jednokrokowymi. Jak widać ich własności nie są rewelacyjne - istnieje wiele schematów o dużo lepszych własnościach.