Grupy izometrii prostokąta i kwadratu
Naturalnych przykładów grup dostarcza geometria.
Rozważmy na płaszczyźnie dowolny prostokąt i izometrie płaszczyzny przekształcające ten prostokąt na ten sam prostokąt.
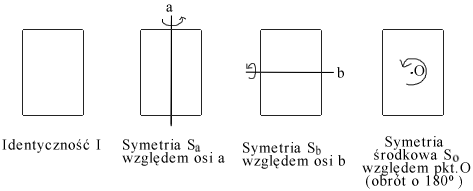
Pamiętamy, że składanie przekształceń jest łączne. Ponadto
nietrudno sprawdzić, że składając dowolne dwie izometrie
prostokąta otrzymamy także pewną jego izometrię. Zatem zbiór 
wraz z działaniem składania przekształceń jest
grupą. Elementem neutralnym jest przekształcenie identycznościowe
, a elementem odwrotnym dowolnego przekształcenia jest to samo
przekształcenie.
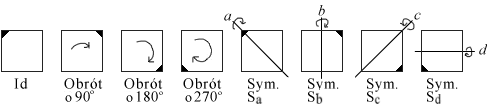
Podobnie rzecz się ma dla kwadratu, którego wszystkie 8 izometrii
własnych pokazanych jest na rysunku poniżej.
[ Początek strony ] [ MiNIWykłady ]