Grupy permutacji


Permutacja
Permutacją zbioru $A$ nazywamy różnowartościowe przekształcenie zbioru skończonego $A$ na zbiór $A$.
Wśród grup skończonych na szczególną uwagę zasługują grupy permutacji. Permutacje $n$-elementowego zbioru $\{1,2,,n\}$ wraz z działaniem składania przekształceń tworzą grupę przekształceń o $n!$ elementach. Będziemy ją oznaczać przez $S_n$.

Permutację $\sigma$ wygodnie jest zilustrować w następujący sposób:
\begin{displaymath}1\mapsto \sigma(1)\end{displaymath}
\begin{displaymath}2\mapsto \sigma(2)\end{displaymath}
\begin{displaymath}\vdots\end{displaymath}
\begin{displaymath}n\mapsto \sigma(n)\end{displaymath}
Na przykład permutacja$\sigma$:
\begin{displaymath}1\mapsto 4\end{displaymath}
\begin{displaymath}2\mapsto 1\end{displaymath}
\begin{displaymath}3\mapsto 2\end{displaymath}
\begin{displaymath}4\mapsto 3\end{displaymath}
\begin{displaymath}5\mapsto 5\end{displaymath}

jest przekształceniem, w którym obrazem elementu 1 jest 4, obrazem 2 jest 1, obrazem 3 jest 2, obrazem 4 jest 3 a obrazem 5 jest 5.

Elementem neutralnym w grupie jest permutacja identycznościowa, która przyporządkowuje każdemu elementowi zbioru $A$ ten sam element.
\begin{displaymath}1\mapsto 1\end{displaymath}
\begin{displaymath}2\mapsto 2\end{displaymath}
\begin{displaymath}\vdots\end{displaymath}
\begin{displaymath}n\mapsto n\end{displaymath}

Taki zapis umożliwia łatwe znalezienie permutacji odwrotnej. Wystarczy tylko zmienić skierowanie strzałek. Na przykład permutacją odwrotną do permutacji $\sigma$ jest permutacja $\sigma'$:
\begin{displaymath}4\mapsto 1\end{displaymath}
\begin{displaymath}1\mapsto 2\end{displaymath}
\begin{displaymath}2\mapsto 3\end{displaymath}
\begin{displaymath}3\mapsto 4\end{displaymath}
\begin{displaymath}5\mapsto 5\end{displaymath}

Czyli po uporządkowaniu permutacja $\sigma'$ ma postać
\begin{displaymath}1\mapsto 2\end{displaymath}
\begin{displaymath}2\mapsto 3\end{displaymath}
\begin{displaymath}3\mapsto 4\end{displaymath}
\begin{displaymath}4\mapsto 1\end{displaymath}
\begin{displaymath}5\mapsto 5\end{displaymath}

Ponadto składanie permutacji ustalonego zbioru jest także permutacją tego zbioru. Zatem zbiór wszystkich permutacji n-elementowego zbioru jest rzeczywiście grupą.

Oznaczmy w trójkącie równoramiennym wierzchołki cyframi $1, 2$ i $3$.

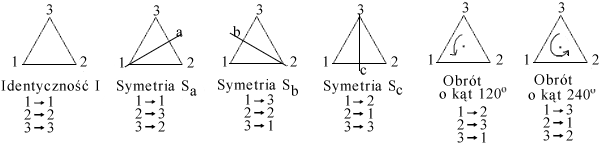
Zauważmy, że dowolna izometria własna tego trójkąta może być interpretowana jako przestawienie tychże cyfr, czyli jako permutacja zbioru $\{1,2,3\}$. Odległe, wydawałoby się, grupy okazały się identyczne. Podobnie grupy symetrii prostokąta i kwadratu są identyczne z pewnymi podzbiorami grupy permutacji zbioru czteroelementowego.

Tw. Cayley'a
Każda grupa skończona jest (w pewnym sensie) identyczna z podzbiorem pewnej grupy permutacji. Wynik ten znany jest jako twierdzenie Cayley'a i podkreśla ważność grup permutacji w teorii grup.


[ Początek strony ] [ MiNIWykłady ]

Wszystkie prawa zastrzeżone © 2000 Wydział Matematyki i Nauk Informacyjnych Politechniki Warszawskiej