Grupy obrotów w przestrzeni trójwymiarowej

W przeciwieństwie do sytuacji na płaszczyźnie, istnieje tylko 5 wielościanów foremnych w przestrzeni trójwymiarowej. Są to tzw. bryły platońskie:

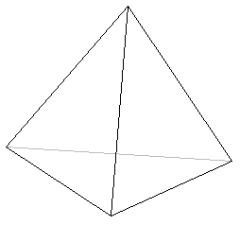czworościan foremny (tetraedr)

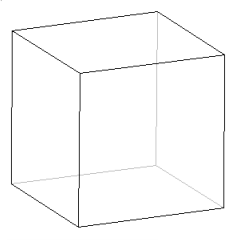sześcian (heksaedr)

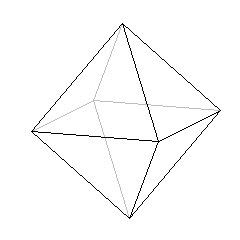ośmiościan (oktaedr)

dwunastościan (dodekaedr), którego ścianami są pięciokąty foremne


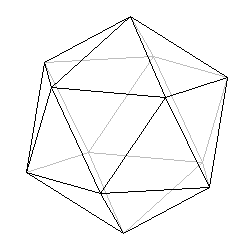
dwudziestościan (ikosaedr), ograniczony przez 20 trójkątów foremnych.


Analogicznie jak dla wielokątów, dla każdej bryły foremnej możemy utworzyć grupę złożoną z obrotów właściwych, które przekształcają bryłę na nią samą. W ten sposób uzyskujemy jednak nie pięć, a tylko trzy różne grupy obrotów. Dla ośmiościanu i sześcianu a także dla dwunastościanu i dwudziestościanu otrzymane grupy są jednakowe. Łatwo to wytłumaczyć. Jeśli połączymy odcinkami środki sąsiednich ścian sześcianu, otrzymamy ośmiościan wpisany w sześcian. Każdy obrót przeprowadzający sześcian na siebie przeprowadza również ośmiościan na siebie i na odwrót. Analogiczny fakt ma miejsce dla pary dwunastościan - dwudziestościan.

Obroty czworościanu
Grupa obrotów właściwych czworościanu składa się z 12 elementów i zawiera oprócz jedności grupy: 4 obroty o $120^\circ$, 4 obroty o $240^\circ$ i 3 obroty o $180^\circ$. Natomiast grupa obrotów właściwych sześcianu składa się z 24 elementów a dwunastościanu z 60 obrotów.


Inne rodzaje grup obrotów właściwych w przestrzeni uzyskujemy bezpośrednio z obrotów na płaszczyźnie.

Obrót niewłaściwy
Przykładem obrotu niewłaściwego w przestrzeni jest odbicie względem punktu $O$, które przekształca punkty $P$ w ich antypody $P'$. (Aby znaleźć punkt $P'$, łączymy $P$ z $O$ i przedłużamy odcinek $PO$ o jego długość.)


Pełna (nieskończona) lista wszystkich skończonych grup obrotów (właściwych i niewłaściwych) w przestrzeni obejmuje 14 typów grup.


[ Początek strony ] [ MiNIWykłady ]

Wszystkie prawa zastrzeżone © 2000 Wydział Matematyki i Nauk Informacyjnych Politechniki Warszawskiej