Pole dywanu Sierpińskiego

Jakie jest pole powierzchni dywanu Sierpińskiego?

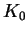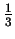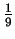Długość boku kwadratu wynosi np. 1. W pierwszym kroku usuwamy 1 kwadrat o długości boku $\frac{1}{3}$ , zatem jego pole jest równe $\frac{1}{9}$ .

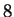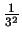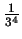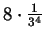W drugim kroku usuwamy kwadratów o długości boku $\frac{1}{3^2}$ . Pole powierzchni każdego z nich jest równe $\frac{1}{3^4}$ . Suma pól powierzchni kwadratów usuniętych w drugim kroku wynosi $8\cdot \frac{1}{3^4}$ .

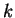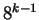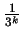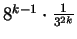W kroku usuwamy $8^{k-1}$ kwadratów o długości boku $\frac{1}{3^k}$ . Zatem ich łączne pole wynosi $8^{k-1}\cdot \frac{1}{3^{2k}}$ .

Po 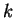krokach suma pól usuniętych kwadratów jest równa
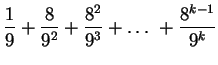
$\displaystyle \frac{1}{9}+ \frac{8}{9^2}+\frac{8^2}{9^3}+\ldots\ +\frac{8^{k-1}}{9^k}$
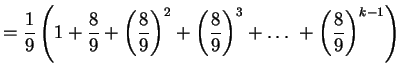
$\displaystyle = \frac{1}{9}\left(1+\frac{8}{9}+ \left(\frac{8}{9}\right)^2 +\left(\frac{8}{9}\right)^3+\ldots\ +\left(\frac{8}{9}\right)^{k-1}\right)$

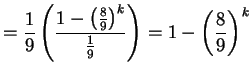
$\displaystyle =\frac{1}{9}\left(\frac{1-\left(\frac{8}{9}\right)^{k}}{\frac{1}{9}}\right)=1-\left(\frac{8}{9}\right)^{k}$

Ciąg geometryczny

Ciąg liczbowy 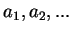jest ciągiem geometrycznym, jeżeli każdy wyraz ciągu (oprócz pierwszego!) jest iloczynem poprzedniego wyrazu przez ustaloną liczbę 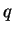. Liczba 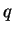nazywana jest ilorazem ciągu geometrycznego.
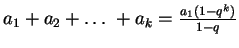
Suma skończenie wielu wyrazów ciągu geometrycznego: $a_1+a_2+\ldots\ +a_{k}=\frac{a_1(1-q^k)}{1-q}$

Przypomnijmy, że dywan Sierpińskiego otrzymamy po nieskończenie wielu krokach - czyli po usunięciu nieskończenie wielu kwadratów. Suma pól powierzchni wszystkich usuniętych kwadratów wynosi

$\displaystyle \lim_{k\to \infty} \left[ 1-\left(\frac{8}{9}\right)^{k}\right]= 1- \lim_{k\to \infty} \left(\frac{8}{9}\right)^{k}=1$

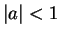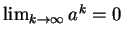
Jeżeli $\vert a\vert<1$ to $\lim_{k\to \infty}\vert a\vert^k=0$

Aby policzyć pole powierzchni dywanu Sierpińskiego należy od pola powierzchni kwadratu 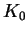odjąć sumę pól powierzchni wszystkich usuniętych kwadratów - czyli
$\displaystyle 1-\lim_{k\to \infty} \left[ 1-\left(\frac{8}{9}\right)^{k}\right]=1-1=0$

Zatem pole powierzchni dywanu Sierpińskiego jest równe 0.

[ Początek strony ] [ MiNIWyklady ]
Wszystkie prawa zastrzeżone © 2000 Wydział Matematyki i Nauk Informacyjnych Politechniki Warszawskiej