Krzywa Kocha Jaka jest długość krzywej Kocha?

Przyjmijmy, że długość boku trójkąta, którego użyliśmy do konstrukcji płatka śniegu, jest równa 1. W pierwszym kroku zastępujemy każdy bok o długości 1 czterema bokami o długości $ \frac{1}{3}$, mamy więc łamaną o długości $ 3\cdot 4\cdot \frac{1}{3}$. W drugim kroku mamy $ 3\cdot 4^2$ boków długości $ \frac{1}{3^2}$, a więc łamana ma długość równą $ 3\cdot 4^2\cdot \frac{1}{3^2}$, czyli $ 3\cdot\left(\frac{4}{3} \right)^2 $. W trzecim kroku liczba boków gwiazdki wzrosła do $ 3\times 4^3$, a długość każdego boku zmalała do $ \frac{1}{3^3}$. Cała gwiazdka ma więc obwód równy $ 3\cdot\left(\frac{4}{3} \right)^3 $. Po $ k$ krokach liczba boków gwiazdki jest równa $ 3\cdot {4}^k$ a długość boku wynosi $ \frac{1}{3^k}$. Obwód gwiazdki jest zatem równy $ 3\cdot \left(\frac{4}{3}\right)^k$. W każdym następnym kroku obwód gwiazdki rośnie. Gdy $ k$ dąży do nieskończoności, to ciąg liczb postaci $ \left(\frac{4}{3}\right)^k$ dąży do nieskończoności, a więc

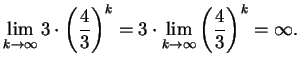
$\displaystyle \lim_{k\to \infty} 3\cdot \left(\frac{4}{3}\right)^k= 3\cdot \lim_{k\to \infty} \left(\frac{4}{3}\right)^k=\infty.$

Naturalnym jest więc przyjąć, że długość krzywaj Kocha jest równa nieskończoność.


[ Początek strony ] [ MiNIWyklady ]

Wszystkie prawa zastrzeżone © 2000 Wydział Matematyki i Nauk Informacyjnych Politechniki Warszawskiej