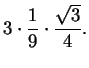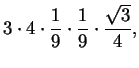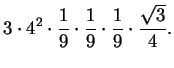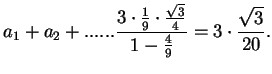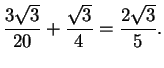Jakie jest pole płatka śniegu ?
Przyjmijmy znów, że bok trójkąta od którego zaczynamy
konstrukcję płatka ma długość równą 1, czyli pole trójkąta
jest równe
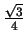 . W pierwszym kroku dorzucamy
trzy trójkąty równoboczne o długości boku
. W pierwszym kroku dorzucamy
trzy trójkąty równoboczne o długości boku
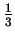 .
Każdy z dorzuconych trójkątów ma więc pole
dziewięciokrotnie mniejsze niż początkowy trójkąt; a więc do
poprzedniego pola należy dorzucić
.
Każdy z dorzuconych trójkątów ma więc pole
dziewięciokrotnie mniejsze niż początkowy trójkąt; a więc do
poprzedniego pola należy dorzucić
Przypomnijmy, że gwiazdka ma teraz 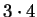 boki. Popatrzmy na to, co dzieje się w następnym kroku.
Każdy bok 'rodzi' mniejszy trójkącik. Boki trójkątów maleją
trzykrotnie, a więc ich pola maleją dziewięciokrotnie. Do pola
obliczonego przed chwilą trzeba dorzucić pola 12 nowych
trójkącików, czyli
a boków mamy teraz
boki. Popatrzmy na to, co dzieje się w następnym kroku.
Każdy bok 'rodzi' mniejszy trójkącik. Boki trójkątów maleją
trzykrotnie, a więc ich pola maleją dziewięciokrotnie. Do pola
obliczonego przed chwilą trzeba dorzucić pola 12 nowych
trójkącików, czyli
a boków mamy teraz
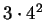 . I co dalej?
Znów z każdego takiego boku powstanie trójkącik o polu
dziewięć razy mniejszym niż poprzednio i trzeba dorzucić
Możemy już spróbować
odgadnąć regułę dorzucania pól. Trzeba poprzedni wynik
mnożyć przez 4, bo tyle razy rośnie liczba boków, i dzielić
przez 9, bo tyle razy maleje pole trójkąta. Krótko mówiąc,
poprzedni wynik mnożymy przez
. I co dalej?
Znów z każdego takiego boku powstanie trójkącik o polu
dziewięć razy mniejszym niż poprzednio i trzeba dorzucić
Możemy już spróbować
odgadnąć regułę dorzucania pól. Trzeba poprzedni wynik
mnożyć przez 4, bo tyle razy rośnie liczba boków, i dzielić
przez 9, bo tyle razy maleje pole trójkąta. Krótko mówiąc,
poprzedni wynik mnożymy przez
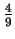 . Otrzymaliśmy
więc, że kolejno dorzucane pola tworzą ciąg geometryczny o
ilorazie równym
. Otrzymaliśmy
więc, że kolejno dorzucane pola tworzą ciąg geometryczny o
ilorazie równym
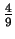 . Iloraz tego ciągu jest liczbą
dodatnią, mniejszą od 1, a więc istnieje suma nieskończenie
wielu wyrazów tego ciągu geometrycznego.
. Iloraz tego ciągu jest liczbą
dodatnią, mniejszą od 1, a więc istnieje suma nieskończenie
wielu wyrazów tego ciągu geometrycznego.
|
Ciąg liczbowy 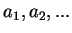 jest ciągiem geometrycznym, jeżeli każdy wyraz ciągu (oprócz pierwszego!)
jest iloczynem poprzedniego wyrazu przez ustaloną liczbę
jest ciągiem geometrycznym, jeżeli każdy wyraz ciągu (oprócz pierwszego!)
jest iloczynem poprzedniego wyrazu przez ustaloną liczbę
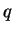 .
Liczba .
Liczba 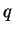 nazywana jest ilorazem ciągu geometrycznego nazywana jest ilorazem ciągu geometrycznego
|
|
|
Pole pierwszego trójkąta nie pasuje do tej reguły. To nic nie
szkodzi. Zaczniemy sumowanie od wyrazu
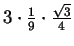 i to będzie u nas
i to będzie u nas 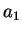 . Tak więc
. Tak więc
|
Suma nieskończenie wielu wyrazów ciągu geometrycznego
|
Jeżeli 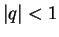 , to , to
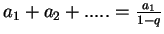 |
|
|
Na koniec dorzućmy pole wyjściowego trójkąta, które
pominęliśmy w sumowaniu, a otrzymamy
Ta końcowa liczba to pole płatka śniegu.
[ Początek strony ]
[ MiNIWyklady ]
 Wszystkie prawa zastrzeżone © 2000 Wydział Matematyki i Nauk Informacyjnych Politechniki Warszawskiej
Wszystkie prawa zastrzeżone © 2000 Wydział Matematyki i Nauk Informacyjnych Politechniki Warszawskiej
![]() . W pierwszym kroku dorzucamy
trzy trójkąty równoboczne o długości boku
. W pierwszym kroku dorzucamy
trzy trójkąty równoboczne o długości boku
![]() .
Każdy z dorzuconych trójkątów ma więc pole
dziewięciokrotnie mniejsze niż początkowy trójkąt; a więc do
poprzedniego pola należy dorzucić
.
Każdy z dorzuconych trójkątów ma więc pole
dziewięciokrotnie mniejsze niż początkowy trójkąt; a więc do
poprzedniego pola należy dorzucić