Jak to się zaczęło - czyli mosty królewieckie
Prawie każdy wykład z Teorii Grafów zaczyna się tak:
W osiemnastym wieku mieszkańcy Królewca lubili spacerować po mostach na rzece Pregole, których mieli w mieście siedem. Plan mostów pokazuje rysunek.
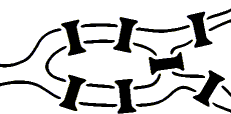
Ale takie zwykłe spacerowanie po jakimś czasie im się znudziło, i zaczęli zastanawiać się, czy jest taka trasa spacerowa, która przechodzi przez każdy most dokładnie raz, żadnego nie omija, i pozwala wrócić do punktu wyjścia.
Nie potrafili sami rozwiązać tego problemu, więc napisali do znanego już wtedy matematyka Leonharda Eulera. Euler pokazał, że nie istnieje rozwiązanie tego zadania. (Jeśli wejdzie się po raz trzeci na wyspę, nie ma jak z niej wyjść.)
Można tę sytuację przedstawić jako graf o wielokrotnych krawędziach:
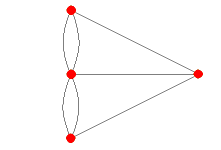
Trzeba w tym grafie znaleźć cykl Eulera, czyli cykl przechodzący przez wszystkie wierzchołki i wszystkie krawędzie tego grafu, ale przez każdą krawędź tylko raz.
W opublikowanej w 1736 roku pracy Euler sformułował pierwsze twierdzenie teorii grafów, które dziś zapisujemy następująco:
W grafie można znaleźć cykl Eulera wtedy i tylko wtedy, gdy graf jest spójny i każdy jego wierzchołek ma parzysty stopień.
Znając to twierdzenie zawsze można stwierdzić, czy łamigłówka typu "narysuj figurę nie odrywając ołówka od kartki" ma rozwiązanie.
Fleury podał algorytm, który pozwala znaleźć cykl Eulera w każdym grafie, w którym on istnieje.
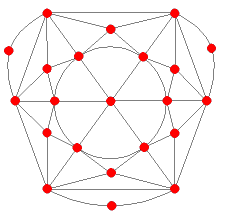
??? Spróbuj samodzielnie znaleźć cykl Eulera w poniższym grafie.
[ Początek strony ] [ MiNIWykłady ]