Problem kojarzenia małżenstw

Dlaczego kojarzenia małżenstw?
Załóżmy, że mamy $k$ kawalerów i $p$ panien oraz dla każdej z panien podany jest zbiór kawalerów, których zna.

Czy jest możliwe wydanie za mąż każdej z kobiet za kawalera, którego zna ?

Sformułowanie przy pomocy grafów.
Zbudujmy graf, którego zbiór wierzchołków składa się z dwóch rozłącznych podzbiorów: zbioru kawalerów $K$ i zbioru panien $P$. Wierzchołek $x$ ze zbioru $K$ łączymy krawędzia z wierzchołkiem $y$ z $P$ jeśli panna $y$ zna kawalera $x$.W otrzymanym grafie nie istnieją krawędzie między żadnymi dwoma wierzchołkami ze zbioru $P$ ani żadnymi dwoma ze zbioru $K$. Jest to więc graf dwudzielny. Poszukiwany jest w tym grafie zbiór krawędzi $M$ taki, że:

1. żadna para krawędzi należących do $M$ nie ma wspólnego wierzchołka (małżenstwa są rozłączne - nie dopuszczamy bigamii!!!),

2. każdy wierzchołek ze zbioru $P$ jest koncem pewnej krawędzi ze zbioru $M$(każda panna wychodzi za mąż).

Zbiór krawędzi spełniający takie warunki nazywamy skojarzeniem doskonałym.

Kiedy rozwiązanie problemu kojarzenia małżenstw istnieje ?
P. Hall sformułował i udowodnił w 1935 roku twierdzenie, które podaje warunek konieczny i dostateczny na to by problem kojarzenia małżenstw miał rozwiązanie.

Twierdzenia Halla
Problem kojarzenia małżenstw ma rozwiązanie wtedy, gdy każde $m$ panien zna łącznie co najmniej $m$ kawalerów, dla $m=1,2,\; ...p$.

Przykład.
Oto przykładowy graf dla zbioru $P$ złożonego z trzech panien i zbioru $K$ złożonego z trzech kawalerów.

Każda z panien zna dokładnie dwóch kawalerów. Skojarzenie doskonałe istnieje i może wyglądać następująco:

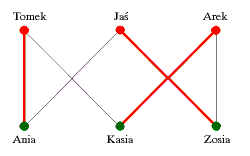
Ania powinna wyjść za Tomka, Kasia za Arka a Zosia za Jasia. Popatrzmy teraz na następujący graf.

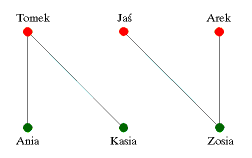
W tym grafie skojarzenie doskonałe nie istnieje. Ania i Kasia znają tylko Tomka. Nie uda sie więc znaleźć równocześnie męża dla obydwu panien.

Zastosowania.
Problem ten posiada bardziej poważne zastosowania. Przy użyciu tej samej metody możemy rozwiązać problem polegający na przydzieleniu pracownikom zajęć zgodnie z ich kwalifikacjami. W tym przypadku przez $P$ należy rozumieć zbiór pracowników, $K$zbiór zadan do wykonania. Dwa wierzchołki $x$ i $y$ łączymy krawędzią jeśli praca $y$ jest zgodna z kwalifikacjami pracownika $x$ (to znaczy może on ją wykonywać).

[ Początek strony ] [ MiNIWykłady ]

---

Wszystkie prawa zastrzeżone © 2000 Wydział Matematyki i Nauk Informacyjnych Politechniki Warszawskiej