W celu obliczenia wymiaru Minkowskiego piramidy Sierpińskiego F pokrywamy ją dostatecznie małymi kostkami (ostrosłupami regularnymi) o boku długości e i wyznaczamy ich liczbę Ne (F ).
Kostka o boku długości 1 pokrywa całą piramidę Sierpińskiego.
e =1 Ne (F )=1
W drugim kroku potrzebujemy 4 kostek o boku długości 1/2, żeby pokryć piramidę Sierpińskiego.
e =1/2 Ne (F )=4

W celu pokrycia piramidy Sierpińskiego kostkami o boku długości 1/4 potrzebujemy 16 ostrosłupów.
e =1/4 Ne (F )=16

e =1/2k Ne (F )=4k

Zmniejszając długość boku kostki, otrzymujemy wzrost liczby kostek potrzebnych do pokrycia piramidy Sierpińskiego.
Policzmy wymiar Minkowskiego
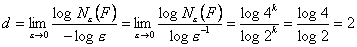
Wymiar piramidy Sierpińskiego wynosi 2. Blok budujący dla tego fraktala jest figurą trójwymiarową, a fraktal ma wymiar Minkowskiego 2. Jak widać na tym przykładzie, przyjęcie definicji, że fraktal to figura, której wymiar Minkowskiego nie jest liczbą naturalną jest błędna.
[ Początek strony ] [ MiNIWyklady ]
Wszystkie prawa zastrzeżone © 2002 Wydział Matematyki i Nauk Informacyjnych Politechniki Warszawskiej