Wymiar z punktu widzenia geometrii klasycznej

Intuicja podpowiada nam, że odcinek powinien mieć wymiar równy 1. Rzeczywiście tak jest, gdyż do opisania położenia dowolnego punktu odcinka wystarczy jedna współrzędna. Odległość punktu od początku odcinka jednoznacznie określa położenie tego punktu na odcinku.

Wymiar punktu Z własności wymiaru wynika, że wymiar punktu lub zbioru złożonego ze skończonej liczby punktów ma wartość zero.

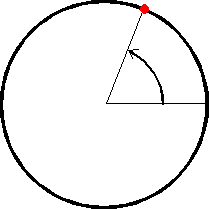
Wymiar okręgu (a nie koła) również wynosi 1. Wystarczy przecież podać kąt, żeby jednoznacznie określić położenie dowolnego punktu okręgu.

Wymiar linii Wymiar każdej linii gładkiej (odcinek, okrąg itp.), łamanej ma wymiar 1. Wystarczy przecież podać odległość punktu od ustalonego początku linii.

Wymiar figur takich jak kwadrat, koło lub brzeg sześciennej kostki wynosi 2. Wszak, żeby zlokalizować punkt na płaszczyźnie trzeba podać dwie współrzędne. Zastanówcie się dlaczego brzeg sześciennej kostki ma również wymiar równy 2.

Podpowiedź Zauważmy, że brzeg sześciennej kostki składa się z 12 odcinków. Wiemy już, że do opisania położenia dowolnego punktu odcinka wystarczy jedna współrzędna. Druga współrzędna potrzebna jest do określenia, na której z 12 krawędzi znajduje się punkt.

Natomiast, w oczywisty sposób, wymiar kostki sześciennej wynosi 3. Tyle współrzędnych potrzeba do opisania położenia punktu w przestrzeni trójwymiarowej.

[ Początek strony ] [ MiNIWyklady ]

---

Wszystkie prawa zastrzeżone © 2002 Wydział Matematyki i Nauk Informacyjnych Politechniki Warszawskiej