Perceptron

Jednym z podstawowych modeli sieci jednokierunkowych jest perceptron przedstawiony na rysunku poniżej. Perceptron zbudowany jest z $N$ neuronów wejściowych i $M$ neuronów wyjściowych. Elementy zarówno wejścia jak wyjścia perceptronu przyjmują wartości binarne, tzn. należą do zbioru $\{0,1\}$.


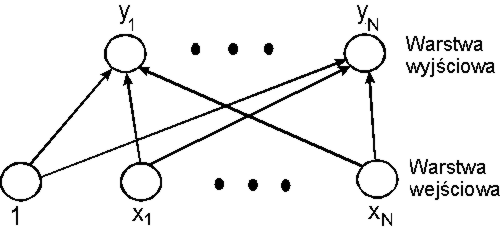
Zadaniem perceptronu jest odwzorowanie zadanego zbioru wektorów wejściowych na zadany zbiór wektorów wyjściowych. W związku z tym zbiór danych uczących składa się z par $(X^i, Y^i), i=1,\ldots,s$, w których $X^i$ jest $N$ elementowym wektorem wejściowym, a $Y^i$ skojarzonym z nim $M$ elementowym wektorem wyjściowym.


Każdy z neuronów $y_k, k=1,\ldots,M$ warstwy wyjściowej oblicza swoją wartość według poniższej zasady:

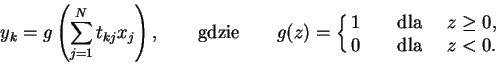\begin{displaymath} y_k=g\left(\sum_{j=1}^N t_{kj} x_j\right),\qquad\textrm{gdz... ...d & dla \quad $z\ge 0$,\cr 0 \quad & dla \quad $z < 0.$ } \end{displaymath} (1)


Proces nauki perceptronu polega na stopniowej modyfikacji wag łączących neurony wejściowe z wyjściowymi w taki sposób, żeby po jego zakończeniu podanie na wejściu któregokolwiek z wektorów $X^i, i=1,\ldots,s$ powodowało wygenerowanie na wyjściu wektora $Y^i$.


 
Uważni czytelnicy zauważyli zapewne, że jeden z neuronów warstwy wejściowej (skrajny lewy) przedstawiony jest nieco inaczej niż pozostałe neurony tej warstwy. Neuron ten jest dodany sztucznie i ma zawsze wartość równą 1.
CZY DOMYŚLACIE SIĘ DLACZEGO? Otóż ten dodany neuron jest niezbędny w sytuacji, w której wektor wejściowy byłby złożony z samych zer, a odpowiadający mu wektor wyjściowy miałby jakieś elementy niezerowe. Bez dodatkowego impulsu wygenerowanie wartości dodatniej na wyjściu przy zerowym wejściu nie byłoby możliwe!


Nauka perceptronu przebiega następująco. W pierwszym kroku wszystkie elementy macierzy wag $T$ są równe zero. Następnie, kolejno pokazywane są pary uczące (według wylosowanej wcześniej kolejności) i po każdej prezentacji wagi perceptronu modyfikowane są według następującego schematu:

\begin{displaymath} t_{ij}(t+1) = t_{ij}(t) + x_j(d_i-y_i), \qquad i=1,\ldots,N,\ \ j=1\ldots,M \end{displaymath} (2)

oraz
\begin{displaymath} t_{i0}(t+1) = t_{i0}(t) + (d_i-y_i), \qquad i=1,\ldots,N. \end{displaymath} (3)


Wszystkie wzorce pokazywane są wielokrotnie, aż do momentu gdy wagi ustabilizują się.

[ Początek strony ] [ MiNIWyklady ]

Wszystkie prawa zastrzeżone © 2000 Wydział Matematyki i Nauk Informacyjnych Politechniki Warszawskiej