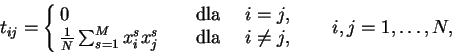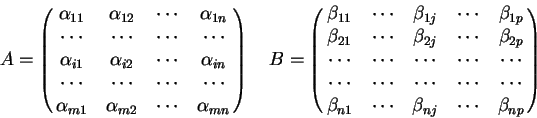Pamięci skojarzeniowe


Wiodącym obszarem zastosowań modelu dyskretnego jest konstruowanie pamięci skojarzeniowych, w których komórki pamięci adresowane są poprzez swoją zawartość a nie za pomocą określonego adresu. Zadaniem pamięci skojarzeniowej jest zapamiętanie danego zbioru wzorców binarnych w taki sposób, żeby po otrzymaniu na wejściu nieznanego wzorca binarnego $X$ pamięć odtwarzała na wyjściu ten z zapamiętanych wzorców, który jest najbliższy $X$ w sensie odległości Hamminga (patrz ramka). Inaczej formułując problem, pamięć skojarzeniowa powinna spełniać dwa warunki:

$(i)$
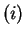
pokazanie na jej wejściu dowolnego z zapamiętanych wektorów (wzorców) powoduje odtworzenie na wyjściu tego samego wektora,
$(ii)$
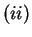
pokazanie na wejściu zaburzonej (,,w rozsądnych granicach'') wersji dowolnego z zapamiętanych wektorów powoduje odtworzenie na wyjściu poprawnej postaci tego wektora.
Odległość Hamminga
 
dla dwóch wektorów binarnych $X$ i $Y$ (ozn. $d_H (X, Y)$ jest równa liczbie bitów, które są różne w tych wzorcach. Na przykład dla $X=[1,0,1,0]$, $Y=[1,1,0,0]$, $d_H(X,Y)=2$, ponieważ wzorce $X$ i $Y$ różnią sie na dwóch pozycjach (drugiej i trzeciej).


Metodę konstruowania pamięci skojarzeniowej podaną przez Hopfielda można streścić następująco. Rozważmy zbiór $\mathcal{X}$ złożony z $M$ wzorców bipolarnych (tzn. o elementach należących do zbioru $\{1,-1\}$) $%% X^i=[x^i_1,\ldots,x^i_N]^T, i=1,\ldots, M$ o długości $N$ każdy.
Transponowanie macierzy
Jeżeli $X$ jest macierzą, to przez $X^T$ oznacza się zwykle macierz transponowaną, której kolejnymi wierszami są kolejne kolumny macierzy $X$, tzn. jeżeli przez $x_{ij}$ oznaczymy element $[i,j]$ macierzy $X$, a przez $x^T_{ij}$ element $[i,j]$ macierzy $X^T$, to zachodzi zależność:
\begin{displaymath} x_{ij} = x^T_{ji} \end{displaymath}

Pamięć skojarzeniowa służąca do zapamiętania wzorców ze zbioru $\mathcal{X}$ zbudowana jest z $N$ neuronów . Kwadratowa macierz połączeń $T$ o wymiarach $N \times N$ obliczana jest za pomocą tzw. reguły Hebba:

\begin{displaymath} t_{ij}=\cases{0 &\quad dla \quad $i=j,$\cr {1\over N} \sum_... ..._j^s &\quad dla \quad $i\ne j,$\cr } \qquad i,j=1,\ldots,N, \end{displaymath} (1)

gdzie $t_{ij}$ jest wagą połączenia wyjścia neuronu $neu_j$ z wejściem neuronu $neu_i$. W zapisie macierzowym powyższa zależność ma postać:
\begin{displaymath} T = {\frac{1}{N}} (XX^T - MI), \end{displaymath} (2)

gdzie $I$ jest macierzą jednostkową wymiaru $N$, a $X$ składa się z $M$ wektorów bazowych zapisanych kolumnowo - $X=[X^1,\ldots, X^M]$.
Mnożenie macierzy
Mnożenie dwóch macierzy: $A$ (o $m$ wierszach i $n$ kolumnach) i $B$ (o $n$ wierszach i $p$ kolumnach) - zauważcie, że liczba kolumn macierzy $A$ musi być równa liczbie wierszy macierzy $B$ - np.


\begin{displaymath} A = \left( \matrix{ \alpha_{11} & \alpha_{12} & \cdots & ... ...a_{n1} & \cdots & \beta_{nj} & \cdots & \beta_{np} }\right)\end{displaymath}

Wynikiem mnożenia $AB$ jest macierz $C$, postaci

\begin{displaymath}C = \left( \matrix{\gamma_{11} & \cdots & \gamma_{1j} & \c... ..._{m1} & \cdots & \gamma_{mj} & \cdots & \gamma_{mp} }\right)\end{displaymath}

której elementy $\gamma_{ij}$ powstają przez pomożenie wiersza $i$ macierzy $A$ przez kolumnę $j$ macierzy $B$. W związku z tym, elementy $\gamma_{ij}$ spełniają zależność:
\begin{displaymath} \gamma_{ij} = \alpha_{i1}\beta_{1j} + \alpha_{i2}\beta_{2j}+\ldots+ \alpha_{in}\beta_{nj} \end{displaymath}

Przykładowo, dla zbioru wzorców $\mathcal{X}%% =\{[1,1,1,1],[1,1,-1,-1],[-1,1,1,-1]\}$ macierz $T$ otrzymana przy zastosowaniu reguły Hebba wygląda następująco:


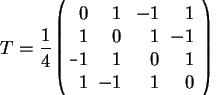
\begin{displaymath}T={\frac{1}{4}} \left\vert\matrix{ \phantom{-}0 & \phantom{-}... ...\phantom{-}1 & -1 & \phantom{-}1 & \phantom{-}0 }\right\vert \end{displaymath}


Rozpoznawanie wzorców z wykorzystaniem nauczonej sieci przebiega w następujący sposób. Nieznany wzorzec $Z=[z_1,\ldots, z_N]$ jest pokazywany w warstwie wejściowej sieci, a następnie wszystkie neurony $_i, i=1\ldots,N$ obliczają swoje potencjały wejściowe $u_i$, oraz wyjściowe $v_i$, tj.

\begin{displaymath} u_i= \sum_{j=1}^N t_{ij} z_j,\quad v_i=g(u_i), \qquad i=1,\ldots,N. \end{displaymath} (3)

Następnie, otrzymany w powyższym układzie równań wektor potencjałów wyjściowych neuronów $[v_1,\ldots,v_N]$ jest podawany ponownie na wejście, liczone są potencjały wejściowe i wyjściowe neuronów, itd. Iteracyjny proces rozpoznawania może zakończyć sie dwojako. Po pierwsze wtedy, gdy sieć osiąga stan stabilny, tj. w dwóch kolejnych iteracjach wygenerowany jest taki sam wektor wyjściowy. Wektor ten jest odpowiedzią sieci na wektor wejściowy $Z$. Drugi sposób zakończenia działania sieci ma miejsce wtedy, gdy zostanie przekroczona zadana z góry liczba iteracji. Sytuacja taka może mieć miejsce w przypadku, gdy sieć oscyluje pomiędzy dwoma stanami, tj. na zmianę generuje na wyjściu dwa różne wektory $A$ i $B$ według schematu:
\begin{displaymath} A\rightarrow B\rightarrow A\rightarrow B\rightarrow\ldots \end{displaymath} (4)

Wracając do naszego przykładu, można łatwo policzyć (zostawiamy to jako ćwiczenie !), że wskazanie na wejściu dowolnego z wektorów $X^1, X^2$ powoduje odtworzenie na wyjściu tego samego wektora i to już w pierwszej iteracji. W przypadku wektora $X^3$ proces rozpoznawania prowadzi do powstania oscylacji z wektorami $A=[-1,1,-1,1], B=[1,-1,1,-1]$.

[ Początek strony ] [ MiNIWyklady ]

Wszystkie prawa zastrzeżone © 2000 Wydział Matematyki i Nauk Informacyjnych Politechniki Warszawskiej