Problem n-hetmanów

Interesującym przykładem problemu kombinatorycznego jest zagadnienie N - hetmanów polegające na ustawieniu na szachownicy N x N, N hetmanów w taki sposób, żeby się wzajemnie nie atakowały.

Wydaje się, że problem jest stosunkowo prosty, ale ... w istocie tak nie jest. Kto nie wierzy - niech spróbuje rozwiązać go np. dla N=20 !

Sieci neuronowe można bardzo efektywnie wykorzystać do rozwiązania tego problemu i problemów podobnych. Odpowiednio zdefiniowana sieć (w omawianym wypadku jest to sieć dyskretna Hopfielda) w kolejnych etapach proponuje przybliżone rozwiązania problemu, by po pewnym czasie osiągnąć rozwiązanie końcowe.

Sieć poszukując rozwiązania często próbuje ustawić inną liczbę hetmanów - np. N-1, ale jest za to karana, co w konsekwencji zmusza ją do przekonfigurowania bieżącego ustawienia w kierunku rozwiązania z N niekolidującymi hetmanami.

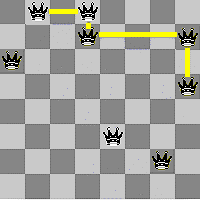
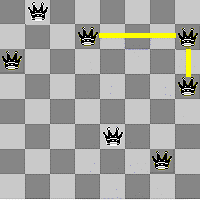
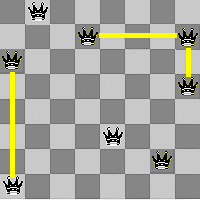
W przypadku N=8 sieć w 1000 prób znajduje rozwiązanie problemu średnio 998 razy !.

Oto przykład funkcjonowania sieci w przypadku standardowej szachownicy 8x8 czyli o 64-ech polach:

Etap Zaproponowane rozwiązanie Liczba kolizji Liczba hetmanów
1 4 8
2 2 7
3 3 8
4 1 7

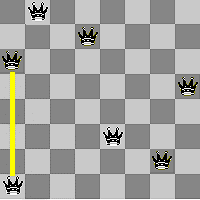
Wreszcie sieć uzyskuje rozwiązanie, spełniające wszystkie założenia, a więc 8 hetmanów ustawionych bez żadnej kolizji:
Jak sprawdzić poprawność rozwiązania ?
Po prostu: w każdym wierszu i w każdej kolumnie musi znajdować się dokładnie jeden hetman, przy czym na żadnej przekątnej nie może być ustawiony więcej niż jeden z nich.

Na koniec zapraszamy do obejrzenia w akcji sieci rozwiązującej problem N-hetmanów w postaci miniprogramu napisanego w języku Java.

[ Początek strony ] [ MiNIWyklady ]

Wszystkie prawa zastrzeżone © 2000 Wydział Matematyki i Nauk Informacyjnych Politechniki Warszawskiej