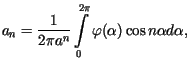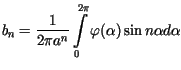Szkic rozwiązania

Jedna z metod rozwiązania oparta jest na przedstawieniu niewiadomej funkcji harmonicznej

w postaci części rzeczywistej pewnej funkcji holomorficznej w kole

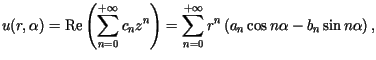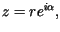
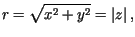
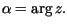$\displaystyle u(r,\alpha)=\operatorname{Re}\left( \sum\limits_{n=0}^{+\infty}c_......imits_{n=0}^{+\infty}r^{n}\left( a_{n}\cos n\alpha-b_{n}\sin n\alpha\right) ,$ gdzie $\displaystyle z=re^{i\alpha},$ $\displaystyle r=\sqrt{x^{2}+y^{2}}=\left\vert z\right\vert ,$ $\displaystyle %%\alpha=\arg z.$ Z warunku brzegowego otrzymujemy, że dla 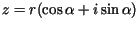$z=r(\cos\alpha+i\sin\alpha)$ musi zachodzić równość 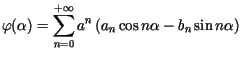$\displaystyle \varphi(\alpha)=\sum\limits_{n=0}^{+\infty}a^{n}\left( a_{n}\cosn\alpha-b_{n}\sin n\alpha\right)$ dla $\displaystyle \alpha\in\lbrack0,2\pi].$ Z własności trygonometrycznych szeregów Fouriera wynika stąd, że 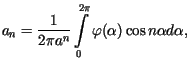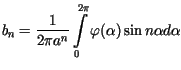$\displaystyle a_{n}=\frac{1}{2\pi a^{n}}\int\limits_{0}^{2\pi}\varphi(\alpha)\cos n\alphad\alpha,$ $\displaystyle b_{n}=\frac{1}{2\pi a^{n}}\int\limits_{0}^{2\pi}\varphi(\alpha)\sin n\alpha d\alpha$ 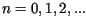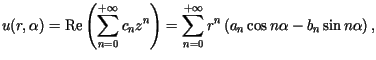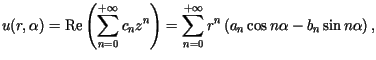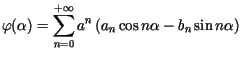dla