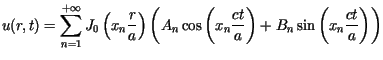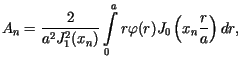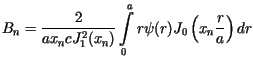Szkic rozwiązania

Z symetrii równania i warunków wynika, że rozwiązanie może być poszukiwane w postaci Przechodząc do współrzędnych biegunowych, przekształcamy wyjściowe równanie do postaci

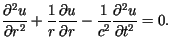
$\displaystyle \frac{\partial^{2}u}{\partial r^{2}}+\frac{1}{r}\frac{\partial u}{\partialr}-\frac{1}{c^{2}}\frac{\partial^{2}u}{\partial t^{2}}=0.$ Stosując metodę Fouriera (rozdzielenia zmiennych) dla

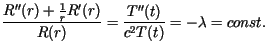
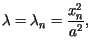otrzymujemy dwa równania $\displaystyle \frac{R^{\prime\prime}(r)+\frac{1}{r}R^{\prime}(r)}{R(r)}=\frac{T^{\prime\prime}(t)}{c^{2}T(t)}=-\lambda=const.$ Z warunków brzegowych wynika, że stały parametr może przyjmować wartości $\displaystyle \lambda=\lambda_{n}=\frac{x_{n}^{2}}{a^{2}},$ dla $\displaystyle n=1,2,...$ gdzie $(x_{n})$ jest ciągiem dodatnich zer funkcji Bessela $J_{0}.$ W takim razie funkcja $\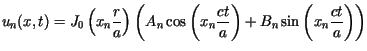displaystyle u_{n}(x,t)=J_{0}\left( x_{n}\frac{r}{a}\right) \left( A_{n}\cos\left(x_{n}\frac{ct}{a}\right) +B_{n}\sin\left( x_{n}\frac{ct}{a}\right) \right)$ dla $\displaystyle n=1,2,...$ i dowolnych stałych $A_{n}$ , $B_{n}$ jest rozwiązaniem rozważanego równania spełniającym jednocześnie warunek brzegowy.

Pełnym rozwiązaniem zagadnienia, spełniającym także warunki początkowe, jest funkcja określona jako suma szeregu

$\displaystyle u(r,t)=\sum\limits_{n=1}^{+\infty}J_{0}\left( x_{n}\frac{r}{a}\ri......ft( x_{n}\frac{ct}{a}\right) +B_{n}\sin\left(x_{n}\frac{ct}{a}\right) \right)$ gdzie stałe $A_{n}$ i $B_{n}$ wyznaczone są za pomocą wzorów $\displaystyle A_{n}=\frac{2}{a^{2}J_{1}^{2}(x_{n})}\int\limits_{0}^{a}r\varphi(r)J_{0}\left( x_{n}\frac{r}{a}\right) dr,$ $\displaystyle B_{n}=\frac{2}{ax_{n}cJ_{1}^{2}(x_{n})}\int\limits_{0}^{a}r\psi(r)J_{0}\left( x_{n}%%\frac{r}{a}\right) dr$ dla