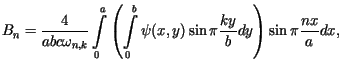Szkic rozwiązania

Stosując metodę Fouriera (rozdzielenia zmiennych) dla otrzymujemy równania

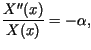
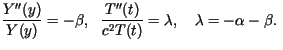
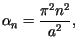
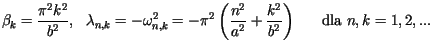
$\displaystyle \frac{X^{\prime\prime}(x)}{X(x)}=-\alpha,$ $\displaystyle \frac{Y^{\prime\prime}%%(y)}{Y(y)}=-\beta,\text{ \ }\frac{T^{\pr......prime}(t)}{c^{2}T(t)}%%=\lambda,\text{ \ \ }\lambda=-\alpha-\beta.\text{\ }%%$ Z warunków brzegowych wynika, że stałe parametry mogą przyjmować wartości $\displaystyle \alpha_{n}=\frac{\pi^{2}n^{2}}{a^{2}},$ $\displaystyle \beta_{k}=\frac{\pi^{2}k^{2}%%}{b^{2}},\text{ \ }\lambda_{n,k}=-......frac{n^{2}}{a^{2}}+\frac{k^{2}}{b^{2}}\right) \text{ \ \ \ \ dla }n,k=1,2,...$ Funkcje postaci $\displaystyle u_{n,k}(x,y,t)=\sin\pi\frac{nx}{a}\sin\pi\frac{ky}{b}\left( A_{n,k}%%\cos(\omega_{n,k}ct)+B_{n,k}\sin(\omega_{n,k}ct)\right)$ są rozwiązaniami równania spełniającymi zadany jednorodny warunek brzegowy.

Pełnym rozwiązaniem zagadnienia, spełniającym także warunki początkowe, jest funkcja określona jako suma szeregu podwójnego

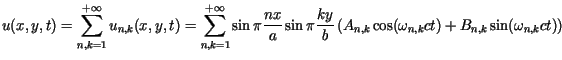
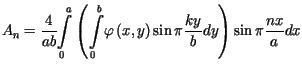$\displaystyle u(x,y,t)=\sum\limits_{n,k=1}^{+\infty}u_{n,k}(x,y,t)=\sum\limits_......c{ky}{b}\left( A_{n,k}\cos(\omega_{n,k}ct)+B_{n,k}\sin(\omega_{n,k}ct)\right)$ gdzie stałe $A_{n}$ i $B_{n}$ wyznaczone są za pomocą wzorów $\displaystyle A_{n}=\frac{4}{ab}%%{\displaystyle\int\limits_{0}^{a}}\left({\......\varphi\left( x,y\right) \sin\pi\frac{ky}{b}dy\right) \sin\pi\frac{nx}%%{a}dx$ , $\displaystyle %%$ $\displaystyle B_{n}=\frac{4}{abc\omega_{n,k}}\int\limits_{0}^{a}\left( \int\limits_{0}%%^{b}\psi(x,y)\sin\pi\frac{ky}{b}dy\right) \sin\pi\frac{nx}{a}dx,$ dla