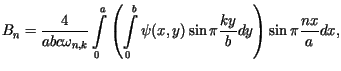Odkształcenie powierzchni sprężystej (membrany)
Odkształcenie powierzchni sprężystej (membrany)![]() opisywane jest równaniem różniczkowym postaci
opisywane jest równaniem różniczkowym postaci
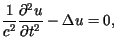
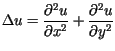
1) ![]()
![]() na brzegu prostokąta
na brzegu prostokąta ![]()
1) ![]()
![]() na brzegu prostokąta
na brzegu prostokąta ![]()
Szkic rozwiązania
Rozwiązaniem zagadnienia, spełniającym warunki początkowe oraz brzegowe,
jest funkcja ![]() określona jako suma szeregu podwójnego
określona jako suma szeregu podwójnego
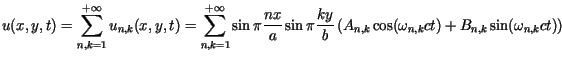
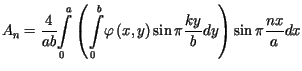 ,
,