Przykład obliczeniowy

Rozwiązać zagadnienie drgań membrany nieograniczonej dla danych:

$\displaystyle c=1,$ $\displaystyle f(x,y)=\frac{1}{1+x^{2}+y^{2}},$ $\displaystyle \varphi(x,y)=0.$ Rozwiązanie

Stosując we wzorze Poissona zamianę zmiennych w całce podwójnej

$\displaystyle p=x+r\cos\alpha$ , $\displaystyle q=y+r\sin\alpha$ otrzymujemy wzór na funkcję

w postaci $\displaystyle u(x,y,t)=\frac{\partial}{\partial t}\left[ \frac{1}{2\pi}\int\lim......}f(x+r\cos\alpha,y+r\sin\alpha)\frac{r}{\sqrt{t^{2}-r^{2}}}drd\alpha\right] =$ $\displaystyle =\frac{\partial}{\partial t}\left[ \frac{1}{2\pi}\int\limits_{0}^......^{2}+2xr\cos\alpha+2yr\sin\alpha}\frac{r}{\sqrt{t^{2}-r^{2}}}drd\alpha\right]$

Animacja - wygląd membrany (268 kB)

Animacja - plan warstwicowy (338 kB)

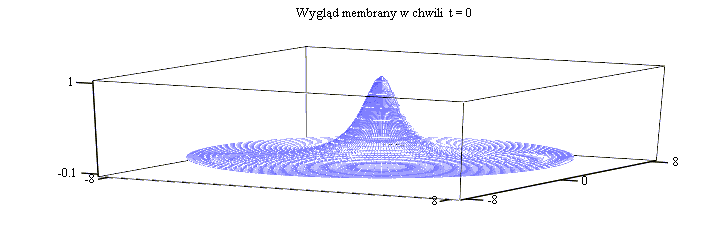
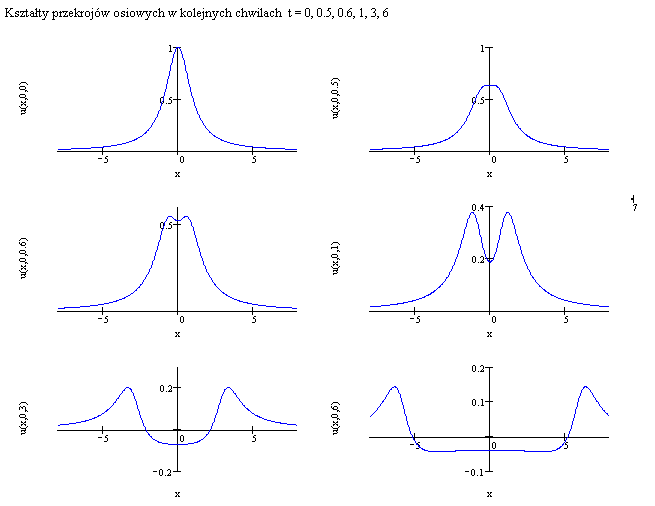
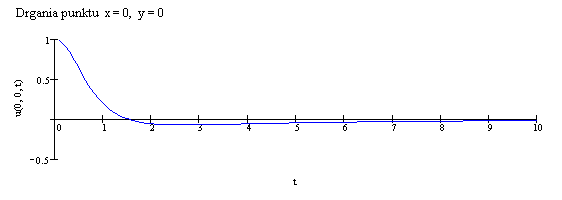
W chwili początkowej wychylenie membrany jest skoncentrowane wokół punktu (0,0). Wychylenie to przemieszcza się na zewnątrz, od chwili t=3 obserwujemy pojawienie sie wyraźnie wypłaszczonego obszaru w otoczeniu początku układu współrzędnych. Obszar ten rozszerza się w czasie. Zjawiska te można zaobserwować w obu animacjach.
Na warstwicach jest zaznaczone odpowiadające im wychylenie, czyli wartość funkcji u.