Odkształcenie powierzchni sprężystej (membrany)
Odkształcenie powierzchni sprężystej (membrany)![]() opisane jest równaniem różniczkowym postaci
opisane jest równaniem różniczkowym postaci
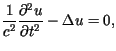
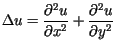
Poszukiwana funkcja ![]() spełnia warunki początkowe postaci
spełnia warunki początkowe postaci
Następujące twierdzenie określa warunki dostateczne dla istnienia rozwiązania i podaje jego postać (tzw. wzór Poissona)
Twierdzenie
Jeżeli funkcje ![]() i
i ![]() są odpowiednio klasy
są odpowiednio klasy![]() i
i ![]() ,
to funkcja
,
to funkcja ![]() postaci
postaci
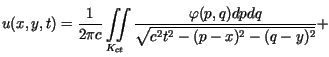
![$\displaystyle +\frac{\partial}{\partial t}\left[ \frac{1}{2\pi c}\iint\limits_{K_{ct}}%%\frac{f(p,q)dpdq}{\sqrt{c^{2}t^{2}-(p-x)^{2}-(q-y)^{2}}}\right]$](img15.gif)