Szkic rozwiązania

Stosując metodę Fouriera (rozdzielenia zmiennych) dla otrzymujemy równanie

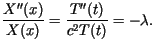
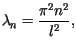$\displaystyle \frac{X^{\prime\prime}(x)}{X(x)}=\frac{T^{\prime\prime}(t)}{c^{2}%%T(t)}=-\lambda.$ Z warunków brzegowych wynika, że stały parametr może przyjmować wartości $\displaystyle \lambda_{n}=\frac{\pi^{2}n^{2}}{l^{2}},$ dla $\displaystyle n=1,2,...$ Funkcje postaci $\displaystyle u_{n}(x,t)=\sin\pi\frac{nx}{l}%%$ są rozwiązaniami równania drgań struny spełniającymi zadany jednorodny warunek brzegowy.

Pełnym rozwiązaniem zagadnienia, spełniającym także warunki początkowe, jest funkcja określona jako suma szeregu

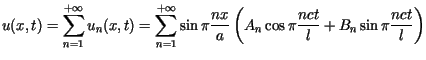
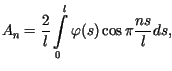
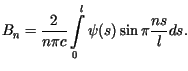
$\displaystyle u(x,t)=\sum\limits_{n=1}^{+\infty}u_{n}(x,t)=\sum\limits_{n=1}^{+......rac{nx}{a}\left( A_{n}\cos\pi\frac{nct}{l}+B_{n}\sin\pi\frac{nct}%%{l}\right)$ gdzie stałe $A_{n}$ i $B_{n}$ wyznaczone są za pomocą wzorów $\displaystyle A_{n}=\frac{2}{l}\int\limits_{0}^{l}\varphi(s)\cos\pi\frac{ns}{l}ds,$ $\displaystyle B_{n}=\frac{2}{n\pi c}\int\limits_{0}^{l}\psi(s)\sin\pi\frac{ns}{l}ds.$ Funkcja

jest okresowa, o okresie równym co najwyżej $\frac{2l}{c}.$

Uwaga

Łatwo pokazać, że w przypadku, gdy $\psi=0,$ rozwiązanie spełniać musi tożsamość

$\displaystyle u(x,t)=-u(l-x,t+\frac{l}{c})$ zaś, gdy $\varphi=0$ zachodzić musi związek $\displaystyle u(x,t)=u(l-x,t+\frac{l}{c}).$