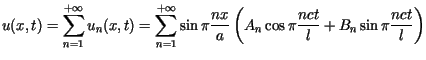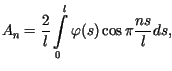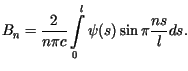Powrót
Struna ograniczona
Równanie drgań ograniczonej struny jednowymiarowej, na którą nie działają
siły zewnętrzne, zapisać można w postaci
![$\displaystyle \frac{1}{c^{2}}\frac{\partial^{2}u}{\partial t^{2}}-\frac{\partial^{2}%%u}{\partial x^{2}}=0\text{ \ \ \ dla }x\in\lbrack0,l],\text{ }t>0,$](img1.gif) gdzie
gdzie 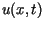 oznacza wychylenie struny z położenia równowagi w punkcie
oznacza wychylenie struny z położenia równowagi w punkcie 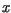 ,
w chwili czasu
,
w chwili czasu 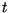 .
Jednorodne warunki brzegowe
.
Jednorodne warunki brzegowe
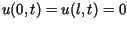 dla
dla 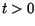 opisują zamocowanie struny na końcach.
opisują zamocowanie struny na końcach.
Zakładamy, że spełnione są warunki początkowe
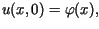
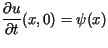 dla
dla ![$\displaystyle x\in\lbrack0,l],$](img9.gif) gdzie funkcje
gdzie funkcje 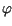 oraz
oraz 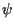 są dane.
są dane.
Szkic rozwiązania
Rozwiązaniem zagadnienia, spełniającym warunki początkowe i brzegowe
jest funkcja 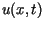 określona jako suma szeregu
określona jako suma szeregu
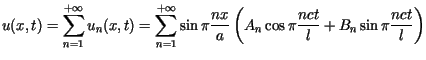 gdzie stałe
gdzie stałe 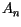 i
i 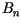 wyznaczone są za pomocą wzorów
wyznaczone są za pomocą wzorów
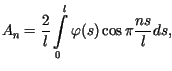
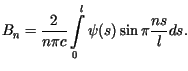
Przykład obliczeniowy 1
Przykład obliczeniowy 2
![$\displaystyle \frac{1}{c^{2}}\frac{\partial^{2}u}{\partial t^{2}}-\frac{\partial^{2}%%u}{\partial x^{2}}=0\text{ \ \ \ dla }x\in\lbrack0,l],\text{ }t>0,$](img1.gif)
![$\displaystyle \frac{1}{c^{2}}\frac{\partial^{2}u}{\partial t^{2}}-\frac{\partial^{2}%%u}{\partial x^{2}}=0\text{ \ \ \ dla }x\in\lbrack0,l],\text{ }t>0,$](img1.gif)
![]() określona jako suma szeregu
określona jako suma szeregu