Powrót
Szkic rozwiązania
Stosując metodę rozdzielenia zmiennych 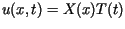 otrzymujemy równość
otrzymujemy równość
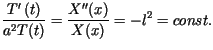 Wynika stąd, że dla dowolnej wartości rzeczywistej parametru
Wynika stąd, że dla dowolnej wartości rzeczywistej parametru 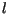 funkcja postaci
funkcja postaci
![$\displaystyle u_{1}(x,t)=\exp\left( -a^{2}l^{2}t\right) \left[ A(l)\cos lx+B(l)\sinlx\right]$](img10.gif) spełnia wyjściowe równanie (być może bez zadanego warunku początkowego).
spełnia wyjściowe równanie (być może bez zadanego warunku początkowego).
Przedstawiając rozwiązanie całego zagadnienia w postaci całki
![$\displaystyle u_{1}(x,t)=\int\limits_{-\infty}^{+\infty}\exp\left( -a^{2}l^{2}t\right)\left[ A(l)\cos lx+B(l)\sin lx\right] dl,$](img11.gif) funkcje
funkcje 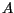 i
i 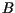 wyznaczamy ze wzorów
wyznaczamy ze wzorów
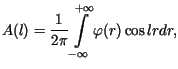
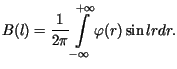 Otrzymane rozwiązanie
Otrzymane rozwiązanie 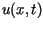 zagadnienia początkowego zapisać można w postaci równoważnej
zagadnienia początkowego zapisać można w postaci równoważnej
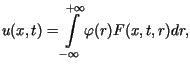 gdzie
gdzie![$\displaystyle F(x,t,r)=\frac{1}{2a\sqrt{\pi t}}\exp\left[ -\frac{\left( r-x\right) ^{2}%%}{4a^{2}t}\right] .$](img18.gif) Z ostatniego wzoru wynika, że w przyjętym modelu zaburzenia cieplne rozchodzą
się z nieskończoną prędkością.
Z ostatniego wzoru wynika, że w przyjętym modelu zaburzenia cieplne rozchodzą
się z nieskończoną prędkością.
![]() otrzymujemy równość
otrzymujemy równość
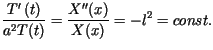
![$\displaystyle u_{1}(x,t)=\int\limits_{-\infty}^{+\infty}\exp\left( -a^{2}l^{2}t\right)\left[ A(l)\cos lx+B(l)\sin lx\right] dl,$](img11.gif)
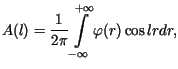
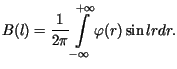
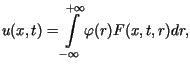 gdzie
gdzie![$\displaystyle F(x,t,r)=\frac{1}{2a\sqrt{\pi t}}\exp\left[ -\frac{\left( r-x\right) ^{2}%%}{4a^{2}t}\right] .$](img18.gif)