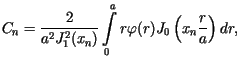Szkic rozwiązania

Stosując metodę Fouriera (rozdzielenia zmiennych) dla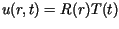

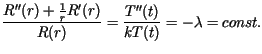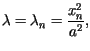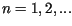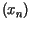otrzymujemy dwa równania $\displaystyle \frac{R^{\prime\prime}(r)+\frac{1}{r}R^{\prime}(r)}{R(r)}=\frac{T^{\prime\prime}(t)}{kT(t)}=-\lambda=const.$ Z warunku brzegowego wynika, że stały parametr może przyjmować wartości $\displaystyle \lambda=\lambda_{n}=\frac{x_{n}^{2}}{a^{2}},$ dla $\displaystyle n=1,2,...$ gdzie $(x_{n})$ jest ciągiem dodatnich zer funkcji Bessela 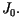$J_{0}.$ W takim razie funkcja 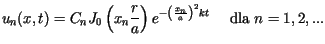$\displaystyle u_{n}(x,t)=C_{n}J_{0}\left( x_{n}\frac{r}{a}\right) e^{-\left( \frac{x_{n}%%}{a}\right) ^{2}kt}\text{ \ \ \ dla }n=1,2,...$ i dowolnej stałej 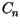$C_{n}$ jest rozwiązaniem rozważanego równania spełniającym jednocześnie jednorodny warunek brzegowy.
Pełnym rozwiązaniem zagadnienia, spełniającym także warunek początkowy, jest funkcja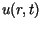

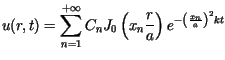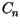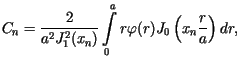
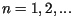
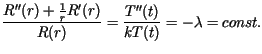
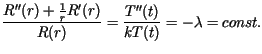
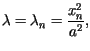określona jako suma szeregu $\displaystyle u(r,t)=\sum\limits_{n=1}^{+\infty}C_{n}J_{0}\left( x_{n}\frac{r}{a}\right)e^{-\left( \frac{x_{n}}{a}\right) ^{2}kt}%%$ gdzie stałe $C_{n}$ wyznaczone są za pomocą wzorów $\displaystyle C_{n}=\frac{2}{a^{2}J_{1}^{2}(x_{n})}\int\limits_{0}^{a}r\varphi(r)J_{0}\left( x_{n}\frac{r}{a}\right) dr,$ $\displaystyle %%$ dla