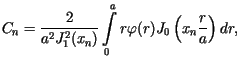Powrót
Zagadnienie I (ostyganie walca)
Rozważamy walec o promieniu 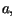 którego osią jest
którego osią jest 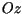 .
Niech
.
Niech 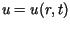 oznacza temperaturę punktu walca oddalonego od jego o
oznacza temperaturę punktu walca oddalonego od jego o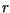 ,
w chwili
,
w chwili 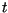 .
Funkcja ta spełnia równanie przewodnictwa postaci
.
Funkcja ta spełnia równanie przewodnictwa postaci
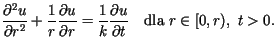 Załóżmy, że powierzchnia boczna walca utrzymywana jest w temperaturze 0,
a więc spełniony jest jednorodny warunek brzegowy
Załóżmy, że powierzchnia boczna walca utrzymywana jest w temperaturze 0,
a więc spełniony jest jednorodny warunek brzegowy
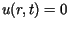 dla
dla 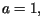
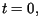 Zakładamy również spełnienie osiowosymetrycznego warunku początkowego
Zakładamy również spełnienie osiowosymetrycznego warunku początkowego
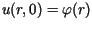 dla
dla 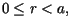 gdzie
gdzie 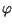 jest funkcją daną, ktora może być przedstawiona w postaci szeregu Fouriera
- Bessela.
jest funkcją daną, ktora może być przedstawiona w postaci szeregu Fouriera
- Bessela.
Szkic rozwiązania
Rozwiązaniem zagadnienia, spełniającym warunek początkowy i brzegowy,
jest funkcja 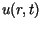 określona jako suma szeregu
określona jako suma szeregu
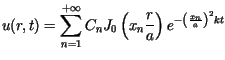 gdzie stałe
gdzie stałe 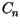 wyznaczone są za pomocą wzorów
wyznaczone są za pomocą wzorów
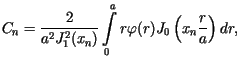
 dla
dla 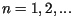
Przykład obliczeniowy
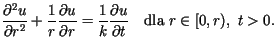
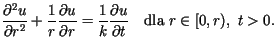
![]() określona jako suma szeregu
określona jako suma szeregu