Powrót
Szkic rozwiązania
Niech 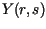 będzie transformatą Laplace'a funkcji
będzie transformatą Laplace'a funkcji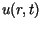 względem zmiennej
względem zmiennej 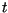 .
Wtedy
.
Wtedy 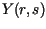 spełnia równanie
spełnia równanie
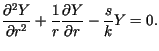 Rozwiązaniem tego równania spełniającym jednocześnie warunek brzegowy jest
funkcja
Rozwiązaniem tego równania spełniającym jednocześnie warunek brzegowy jest
funkcja
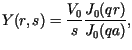 gdzie
gdzie 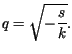 Odwracając transformatę Laplace'a np. za pomocą twierdzenia o residuach,
otrzymujemy ostatecznie wzór na rozwiązanie zagadnienia
Odwracając transformatę Laplace'a np. za pomocą twierdzenia o residuach,
otrzymujemy ostatecznie wzór na rozwiązanie zagadnienia
![$\displaystyle u(r,t)=V_{0}\left[ 1-2\sum\limits_{n=1}^{+\infty}\frac{J_{0}\left......ght) }{x_{n}J_{1}(x_{n})}e^{-\left( \frac{x_{n}}%%{a}\right) ^{2}kt}\right] ,$](img42.gif) gdzie
gdzie 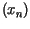 jest ciągiem dodatnich zer funkcji Bessela
jest ciągiem dodatnich zer funkcji Bessela 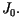
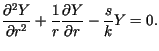
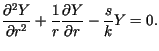
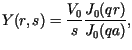 gdzie
gdzie 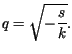
![$\displaystyle u(r,t)=V_{0}\left[ 1-2\sum\limits_{n=1}^{+\infty}\frac{J_{0}\left......ght) }{x_{n}J_{1}(x_{n})}e^{-\left( \frac{x_{n}}%%{a}\right) ^{2}kt}\right] ,$](img42.gif)