Symetria w kryształach
Jednym z ważniejszych zastosowań algebry w naukach przyrodniczych
jest wykorzystanie metod algebraicznych do badania symetrii
różnych układów fizycznych i chemicznych.
Cóż to jest symetria?
Starożytni rozumieli ją jako synonim piękna, harmonii i umiaru,
czegoś co zachowuje właściwe proporcje. Idea za pomocą, której
człowiek starał się tworzyć doskonałość.
|
Symetrie
| |
Ze względu na swoją symetrię koło na płaszczyźnie i kula w
przestrzeni były uważane przez Pitagorejczyków za najdoskonalsze
figury geometryczne. Innymi obiektami geometrycznymi, w których
podziwiamy symetrię są wielokąty foremne.
|
|
|
Z drugim znaczeniem, jakie ma symetria, kojarzy się w naturalny
sposób obraz równowagi na przykład lewego z prawym, widoczny
między innymi w budowie organizmów żywych. Takie pojmowanie
symetrii jest pojęciem czysto geometrycznym.
Na początek przyjrzyjmy się trójkątowi równobocznemu. Znajdźmy
wszystkie izometrie płaszczyzny, które przekształcają ten trójkąt
na ten sam trójkąt (czyli tzw. izometrie własne trójkąta). Będą to
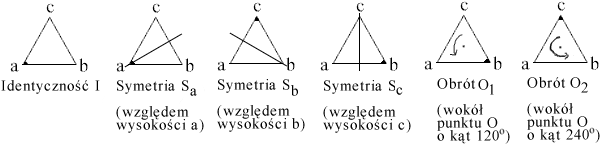
|
Izometria
| |
Izometria (przekształcenie izometryczne) jest to przekształcenie
geometryczne, które zachowuje odległość. To znaczy, że odległość
dowolnych punktów równa jest odległości ich obrazów. Przykładami
izometrii na płaszczyźnie i w przestrzeni są między innymi
przesunięcia równoległe (translacje), obroty, symetrie osiowe czy
też symetrie środkowe. Izometrią jest także odwzorowanie
identycznościowe. Ponadto złożenie dwu izometrii jest również
izometrią.
|
|
|
Nietrudno zauważyć, że złożenie dowolnych dwóch takich izometrii
jest również izometrią trójkąta równobocznego. Ponadto traktując
identyczność jako obrót o 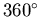 otrzymujemy, że złożenie dwóch dowolnych obrotów trójkąta jest także obrotem.
otrzymujemy, że złożenie dwóch dowolnych obrotów trójkąta jest także obrotem.
Składanie izometrii możemy opisać przy pomocy tabelki. Dla
trójkąta równobocznego ma ona następującą postać:
Możemy z niej odczytać wynik złożenia dowolnych dwóch
przekształceń. Na przykład złożenie obrotu 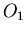 z symetrią
z symetrią 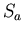 jest symetrią
jest symetrią 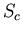 .
.
Zbiór wszystkich obrotów trójkąta równobocznego lub zbiór
wszystkich jego izometrii własnych wraz z operacją składania
przekształceń stanowią przykład struktury, którą matematycy
nazywają grupą. Od tej chwili będziemy zatem mówić o grupach
obrotów, grupach izometrii własnych bądź ogólnie o grupach
przekształceń.
Rozpatrzmy teraz dowolny 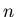 -kąt foremny.
-kąt foremny.
|
|
n-kąt
|
n-kąt foremny to wielokąt o 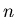 bokach, który ma
wszystkie boki równe i wszystkie kąty między sąsiednimi bokami równe. bokach, który ma
wszystkie boki równe i wszystkie kąty między sąsiednimi bokami równe.
|
|
|
|
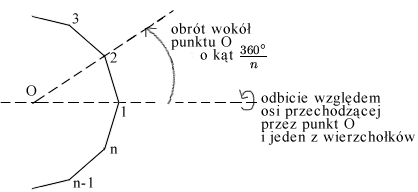
Okazuje się, że grupa 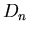 izometrii własnych
izometrii własnych 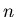 -kąta foremnego
złożona jest z
-kąta foremnego
złożona jest z 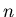 obrotów wokół punktu
obrotów wokół punktu 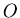 o wielokrotność kąta
o wielokrotność kąta
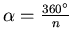 . Są to tak zwane obroty właściwe.
Pozostałe elementy grupy
. Są to tak zwane obroty właściwe.
Pozostałe elementy grupy 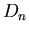 to złożenia obrotów właściwych i
odbicia względem osi przechodzącej przez środek wielokąta oraz
jeden jego wierzchołek. Są to tak zwane obroty niewłaściwe.
Znajomość grupy
to złożenia obrotów właściwych i
odbicia względem osi przechodzącej przez środek wielokąta oraz
jeden jego wierzchołek. Są to tak zwane obroty niewłaściwe.
Znajomość grupy 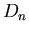 pozwala stwierdzić, że na płaszczyźnie
istnieją dwa rodzaje skończonych grup obrotów. Są to grupy
pozwala stwierdzić, że na płaszczyźnie
istnieją dwa rodzaje skończonych grup obrotów. Są to grupy 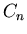 złożone tylko z obrotów właściwych oraz grupy
złożone tylko z obrotów właściwych oraz grupy 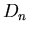 .
.
|
Grupy izometrii
|
Grupa izometrii własnych trójkąta równobocznego oznaczana jest
symbolem 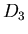 a grupa izometrii własnych kwadratu a grupa izometrii własnych kwadratu 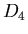 ,
natomiast grupy ich obrotów odpowiednio ,
natomiast grupy ich obrotów odpowiednio 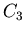 i i 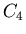 . .
|
|
|
|
Podstawowe grupy
|
Grupa 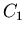 jest jednoelementowa, złożona tylko z identyczności,
grupa jest jednoelementowa, złożona tylko z identyczności,
grupa 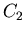 składa się z obrotów o kąt składa się z obrotów o kąt 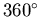 i i 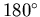 ,
elementami grupy ,
elementami grupy 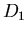 są identyczność i jedna symetria osiowa.
Natomiast grupa są identyczność i jedna symetria osiowa.
Natomiast grupa 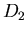 jest identyczna z grupą izometrii własnych
prostokąta. jest identyczna z grupą izometrii własnych
prostokąta.
|
|
|
Jak właśnie zaobserwowaliśmy, wielokąty foremne są powiązane ze
skończonymi grupami obrotów płaskich. Podobnie wielościany foremne
będą powiązane ze
skończonymi grupami obrotów w przestrzeni trójwymiarowej.
Inne fascynujące przykłady symetrii możemy znaleźć w:
Już po tych kilku przykładach możemy się przekonać, że grupy
stanowią potężne narzędzie poznania jednej z największych zasad
otaczającego nas świata - zasady symetrii.
[ Początek strony ]
[ MiNIWykłady ]
 Wszystkie prawa zastrzeżone © 2000 Wydział Matematyki i Nauk Informacyjnych Politechniki Warszawskiej
Wszystkie prawa zastrzeżone © 2000 Wydział Matematyki i Nauk Informacyjnych Politechniki Warszawskiej

![]() z symetrią
z symetrią ![]() jest symetrią
jest symetrią ![]() .
.
![]() -kąt foremny.
-kąt foremny.
