Mówimy, że zbiory Si pokrywają zbiór F, jeżeli każdy element ze zbioru F znajduje się w którymś ze zbiorów Si.
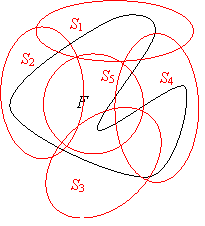
Zauważmy pewną właściwość figur geometrycznych:
Odcinek jest figurą jednowymiarową. Po zwiększeniu dwa razy jego długości otrzymamy figurę 2 = 21 razy większą.
 |
 |
Kwadrat jest figurą dwuwymiarową. Po zwiększeniu dwa razy długości jego boku otrzymamy figurę 4 = 22 razy większą.
 |
 |
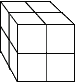
Sześcian jest figurą trójwymiarową. Po zwiększeniu dwa razy długości jego boku otrzymamy figurę 8 = 23 razy większą.
 |
 |
Teraz możemy już stwierdzić, że
Ne (F )=ce -D
gdzie D jest wymiarem Minkowskiego, Ne (F ) jest liczbą zbiorów pokrywających ograniczony zbiór F, c jest stałą, a e jest dokładnością pomiaru (czyli maksymalną średnicą zbiorów pokrywających zbiór F).
Wyznaczmy D.
Logarytmując obie strony otrzymujemy:
log Ne (F )=D log(e) +log(c)
Przekształcając dalej otrzymujemy:
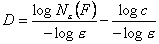
Oczywiście jest to pomiar dla jakiejś dokładności, w związku z czym D jest tylko przybliżone. Aby dokładnie policzyć D bierzemy nieskończenie małe e (korzystamy z definicji granicy):
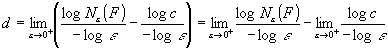
ponieważ c nie zależy od e więc drugi składnik zbiega do zera, więc możemy go opuścić i otrzymujemy:
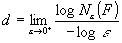
Jeżeli powyższa granica istnieje, to d jest wymiarem Minkowskiego. Istnieją zbiory, dla których powyższa granica nie istnieje. Wspomniany wcześniej wymiar Hausdorffa jest określony dla dowolnego zbioru.
Korzystając z tak sformułowanej definicji bardzo łatwo policzyć wymiar w przybliżeniu, co powoduje iż jest ona bardzo często implementowana w programach komputerowych [zobacz zastosowania].
Równoważne definicje wymiaru Minkowskiego
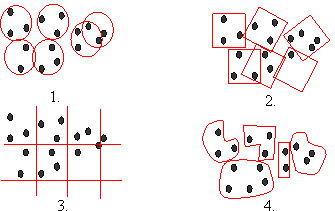
Przeprowadzone rozumowanie nie jest trudne, ale nie odpowiada na jedno pytanie: Jak skonstruować pokrycie mierzonego zbioru? Poniżej podajemy pięć równoważnych sposobów skonstruowania pokrycia zbioru:
- najmniejsza liczba kul o promieniu co najwyżej e pokrywających F;
- najmniejsza liczba kostek o boku e pokrywających F;
- najmniejsza liczba kratek o boku e przecinających F (nałożenie siatki)
- najmniejsza liczba zbiorów o średnicy co najwyżej e pokrywających F.
A oto interpretacja graficzna:
[ Początek strony ] [ MiNIWyklady ]