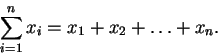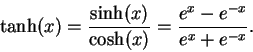Modele sieci

Zadaniem każdego neuronu w sieci jest odbieranie sygnałów otrzymywanych od innych (nie koniecznie wszystkich) neuronów, sumowanie tych sygnałów, przetworzenie sumarycznego sygnału przy zastosowaniu tzw. funkcji aktywacji nazywanej również funkcją transferu albo funkcją przejścia, a następnie wysłanie przetworzonego sygnału do innych neuronów.


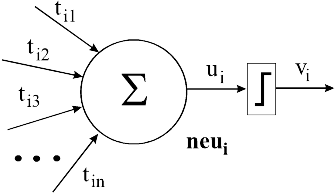
W literaturze opisanych jest wiele modeli neuronów różniących się między sobą przede wszystkim sposobem kolekcjonowania (sumowania)otrzymywanych sygnałów oraz stosowaną funkcją aktywacji decydującą o tym, w którym momencie wysyłany jest sygnał zwrotny i jaka jest moc tego sygnału.

Jednym z fundamentalnych modeli neuronu jest zaproponowany w 1943 roku model McCullocha-Pittsa (ozn. MP). Neuron MP, będący pierwszym formalnie zdefiniowanym modelem neuronu, pomimo zastosowania bardzo dużych uproszczeń w stosunku do modelu neuronu biologicznego (a po części właśnie z tego powodu) znalazł zastosowanie w wielu modelach sieci neuronowych. Schemat neuronu MP przedstawiony jest na rysunku powyżej.

Neurony w sieci komunikują się ze sobą poprzez tzw. połączenia synaptyczne, których wielkość określa waga synaptyczna, nazywana w skrócie wagą. Waga połączenia neuronu z neuronem , oznaczana przez , może mieć wartość

Suma przemnożonych przez wagi sygnałów docierających do neuronu w jednostce czasu stanowi potencjał wejściowy (potencjał wewnętrzny) tego neuronu, oznaczany przez . Odpowiedź neuronu na zadany potencjał wejściowy nazywana jest potencjałem wyjściowym (albo potencjałem zewnętrznym) tego neuronu. Charakterystykę odpowiedzi określa funkcja aktywacji, oznaczana przez . Podstawowym układem równań opisującym działanie neuronu jest w związku z tym:


Znak sumy
znak $\sum_{i=1}^n x_i$ oznacza sumę elementów $x_i$ od $i=1$ do $n$, tzn.
\begin{displaymath} \sum_{i=1}^n x_i = x_1 + x_2 +\ldots + x_n. \end{displaymath}


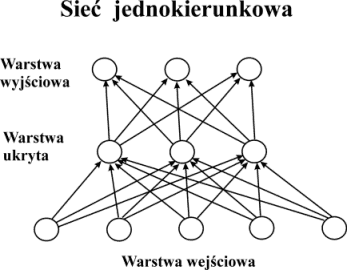
Modele sieci neuronowych różnią się zarówno rodzajem neuronów, z których są zbudowane jak i topologią (układem) połączeń międzyneuronalnych oraz sposobem przesyłania sygnałów w obrębie sieci. Najpopularniejszą grupę stanowią tzw. sieci jednokierunkowe. Sieci te zbudowane są z jednej bądź kilku warstw. Przepływ sygnału w tego typu sieciach przebiega zawsze w ściśle określonym kierunku: od warstwy wejściowej do warstwy wyjściowej. Każda dodatkowa warstwa pomiędzy warstwami wejściową i wyjściową nazywana jest warstwą ukrytą z uwagi na to, że jej działalność nie może być obserwowana bezpośrednio ani na wejściu sieci ani na jej wyjściu.

Na przedstawionym rysunku warstwa wejściowa składa się z 5 neuronów, warstwa ukryta i wyjściowa mają po 3 neurony. Zwykle wszystkie neurony warstwy poprzedniej połączone są ze wszystkimi neuronami warstwy następnej. Połączenia wsteczne, połączenia omijające warstwę oraz połączenia typu sprzężenia zwrotnego (tzn. połączenia neuronu ze sobą) nie występują w sieciach jednokierunkowych. Kierunek przepływu sygnałów zaznaczony jest strzałkami. Najpopularniejszym przykładem sieci jednokierunkowej jest perceptron.

Osobnym problemem jest kwestia zastosowania sieci neuronowej do wykonania określonego zadania. W tym celu stosowane są odpowiednie algorytmy uczące.


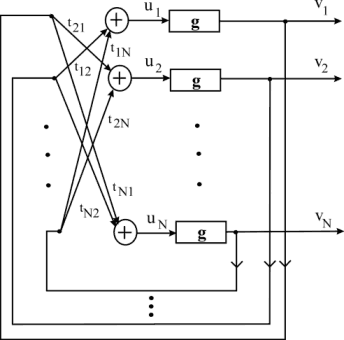
Drugą istotną grupę sieci neuronowych stanowią tzw. sieci rekurencyjne. W sieciach rekurencyjnych sygnał propagowany jest w obiegu zamkniętym, tzn. sygnały z warstwy wyjściowej sieci podawane są z powrotem do warstwy wejściowej. Często, z uwagi na skomplikowaną topologię pojęcie warstwy w sieci rekurencyjnej jest w dużym stopniu umowne. Wejścia sieci mogą być dodatkowo pobudzane wymuszeniem zewnętrznym, które jest sumowane z aktualnym sygnałem w sieci. Jeżeli wymuszenie zewnętrzne jest równe zero, to układ nazywamy autonomicznym.

Najprostsza sieć rekurencyjna składa się z jednej warstwy, w której wyjścia połączone są z wejściami poprzez pętle sprzężeń zwrotnych. Sieć taka, po spełnieniu dodatkowych założeń nazywana jest siecią Hopfielda (por. rysunek powyżej). Sieć dyskretna Hopfielda, tzn. sieć z funkcją przejścia postaci


służy przede wszystkim do konstruowania tzw. pamięci skojarzeniowych.

W sieci ciągłej stosowana jest sigmoidalna funkcja przejścia:


Tangens hiperboliczny
$\tanh$ jest to funkcja tangens hiperboliczny, opisana wzorem
\begin{displaymath} \tanh(x)={{\sinh(x)}\over{\cosh(x)}} = {{e^x -e^{-x}} \over {e^x +e^{-x}}}. \end{displaymath}


Sieć ciągła wykorzystywana jest do rozwiązywania kombinatorycznych problemów optymalizacyjnych.


[ Początek strony ] [ MiNIWyklady ]

Wszystkie prawa zastrzeżone © 2000 Wydział Matematyki i Nauk Informacyjnych Politechniki Warszawskiej