Przykład obliczeniowy

Rozwiązać zagadnienie drgań membrany kołowej dla $\varphi(r)=1-r^{2},$ $\psi(r)=0.$

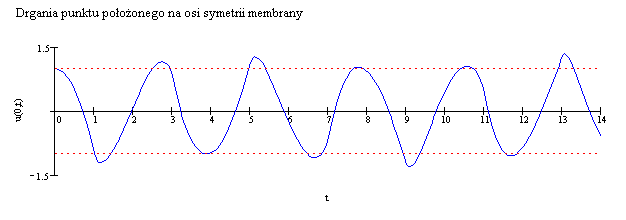
Z tych danych oraz z przytoczonych wzorów (patrz - szkic rozwiązania) wynika, że

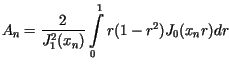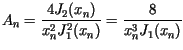
$\displaystyle B_{n}=0,$ $\displaystyle A_{n}=\frac{2}{J_{1}^{2}(x_{n})}\int\limits_{0}%%^{1}r(1-r^{2})J_{0}(x_{n}r)dr$ dla $\displaystyle n=1,2,...$ $\displaystyle %%$ Korzystając z własności funkcji Bessela $\displaystyle \frac{d}{dx}\left[ x^{n}J_{n}(x)\right] =x^{n}J_{n-1}(x)xx$ oraz stosując wzór na całkowanie przez części otrzymujemy ostatecznie $\displaystyle A_{n}=\frac{4J_{2}(x_{n})}{x_{n}^{2}J_{1}^{2}(x_{n})}=\frac{8}{x_{n}^{3}%%J_{1}(x_{n})}%%$ a zatem rozwiązanie zagadnienia wyraża się wzorem $\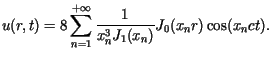displaystyle u(r,t)=8\sum\limits_{n=1}^{+\infty}\frac{1}{x_{n}^{3}J_{1}(x_{n})}J_{0}%%(x_{n}r)\cos(x_{n}ct).$

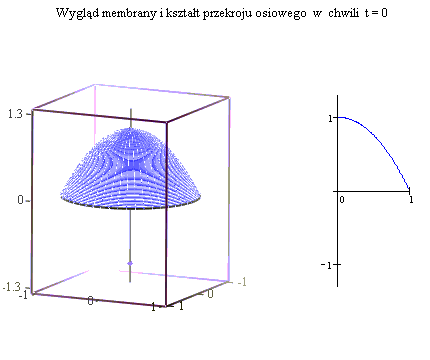
Animacja - wygląd membrany (197 kB)

Animacja - plan warstwicowy (285 kB)

Na warstwicach jest zaznaczone odpowiadające im wychylenie, czyli wartość funkcji u.