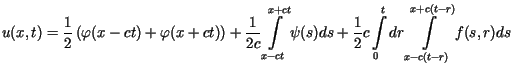Powrót
Struna dwustronnie nieograniczona
Równanie drgań struny jednowymiarowej zapisać można w postaci
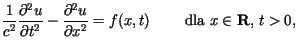 gdzie
gdzie 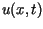 oznacza wychylenie struny z położenia równowagi w punkcie
oznacza wychylenie struny z położenia równowagi w punkcie 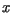 ,
w chwili czasu
,
w chwili czasu 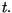 Funkcja
Funkcja 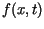 przedstawia gęstość siły zewnętrznej, działającej na strunę.
przedstawia gęstość siły zewnętrznej, działającej na strunę.
Rozwiązując najpierw równanie jednorodne (tzn.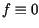 )
i następnie wprowadzając zmienne
)
i następnie wprowadzając zmienne 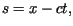
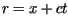 można pokazać, że rozwiązanie daje się przedstawić w postaci tzw. wzoru
d'Alemberta
można pokazać, że rozwiązanie daje się przedstawić w postaci tzw. wzoru
d'Alemberta
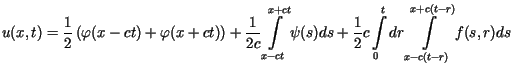 gdzie funkcje
gdzie funkcje 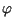 oraz
oraz 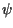 opisują warunki początkowe
opisują warunki początkowe
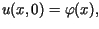
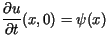 dla
dla 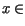 R.
R. Interpretacja fizyczna w przypadku drgań swobodnych
Interpretacja fizyczna w przypadku drgań swobodnych
Przykład obliczeniowy 1
Przykład obliczeniowy 2
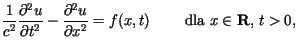
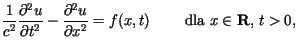
![]() )
i następnie wprowadzając zmienne
)
i następnie wprowadzając zmienne ![]()
![]() można pokazać, że rozwiązanie daje się przedstawić w postaci tzw. wzoru
d'Alemberta
można pokazać, że rozwiązanie daje się przedstawić w postaci tzw. wzoru
d'Alemberta