Przykład obliczeniowy 1

Rozwiązać powyższe zagadnienie początkowe dla oraz $\varphi$ określonej wzorem

$\begin{displaymath}\varphi(x)=\left\{\begin{array}[c]{ll}%%3 & \text{dla }\le......0 & \text{dla }\left\vert x\right\vert >1.\end{array}\right.\end{displaymath}$ Rozwiązanie

Z przedstawionych wzorów (patrz - szkic rozwiązania) wynika, że

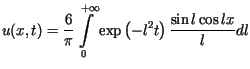
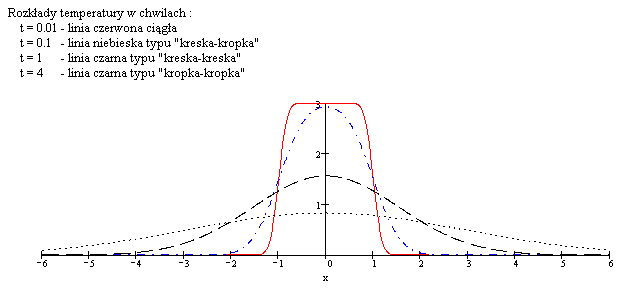
$\displaystyle A(l)=\frac{3\sin l}{l\pi},$ $\displaystyle B(l)=0$ , $\displaystyle %%$ zatem $\displaystyle u(x,t)=\frac{6}{\pi}\int\limits_{0}^{+\infty}\exp\left( -l^{2}t\right)\frac{\sin l\cos lx}{l}dl$ lub w postaci równoważnej $\displaystyle u(x,t)=\frac{3}{\sqrt{\pi t}}\int\limits_{-1}^{+1}\exp\left[ -\frac{\left(r-x\right) ^{2}}{4t}\right] dr.$ Poniższy rysunek przedstawia wykresy temperatury w różnych chwilach czasu.

Dla wartości t bliskich zeru wykres przybliża funkcję $\varphi$ , która jest w tym przykładzie nieciągła, dla dużych t następuje wyrównywanie temperatury wewnątrz pręta.