Przykład obliczeniowy 3

Rozwiązać powyższe zagadnienie początkowe dla oraz $\varphi$ określonej wzorem

$\begin{displaymath}\varphi(x)=\left\{\begin{array}[c]{ll}%%T_{1} & \text{dla }x>0\\T_{2} & \text{dla }x<0.\end{array}\right.\end{displaymath}$ Rozwiązanie

Z przedstawionych wzorów (patrz - szkic rozwiązania) wynika, że

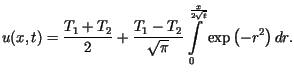
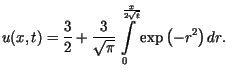
$\displaystyle u(x,t)=\frac{T_{1}+T_{2}}{2}+\frac{T_{1}-T_{2}}{\sqrt{\pi}}\int\limits_{0}%%^{\frac{x}{2\sqrt{t}}}\exp\left( -r^{2}\right) dr.$ W szczególności dla $T_{1}=3,$ $T_{2}=0$ mamy $\displaystyle u(x,t)=\frac{3}{2}+\frac{3}{\sqrt{\pi}}\int\limits_{0}^{\frac{x}{2\sqrt{t}}%%}\exp\left( -r^{2}\right) dr.$ Oto wykresy temperatury.

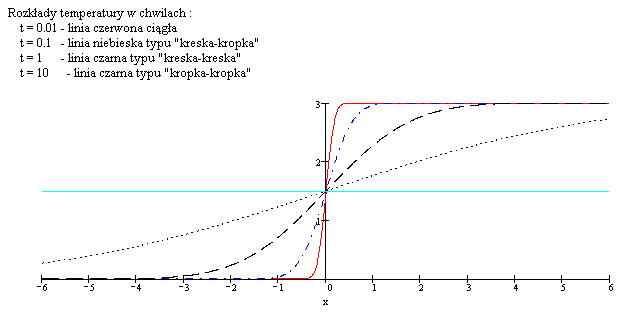
Dla wartości t bliskich zeru wykres przybliża funkcję $\varphi$ , która jest w tym przykładzie nieciągła i nie posiada granicy w punkcie x=0, dla dużych t następuje wyrównywanie temperatury wewnątrz pręta.