Przykład obliczeniowy 3

Rozwiązać powyższe zagadnienie początkowe dla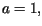

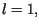
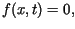
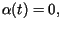
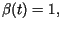
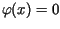$\alpha(t)=0,$ $\beta(t)=1,$ $\varphi(x)=0$ (podgrzewanie pręta od prawego końca).

Rozwiązanie

Z przedstawionych wzorów (patrz - szkic rozwiązania) i warunków zadania wynika, że

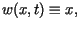
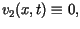
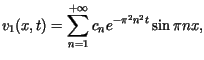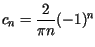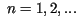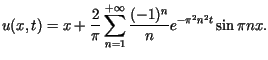$\displaystyle w(x,t)\equiv x,$ $\displaystyle v_{2}(x,t)\equiv0,$ $\displaystyle v_{1}(x,t)=\sum\limits_{n=1}^{+\infty}c_{n}e^{-\pi^{2}n^{2}t}\sin\pi nx,$ gdzie $\displaystyle c_{n}=\frac{2}{\pi n}(-1)^{n}$ dla $\displaystyle \ n=1,2,...$ zatem $\displaystyle u(x,t)=x+\frac{2}{\pi}\sum\limits_{n=1}^{+\infty}\frac{(-1)^{n}}{n}e^{-\pi^{2}n^{2}t}\sin\pi nx.$ Poniższy rysunek przedstawia zmiany wykresu temperatury pręta w czasie oraz temperaturę w punkcie środkowym pręta.

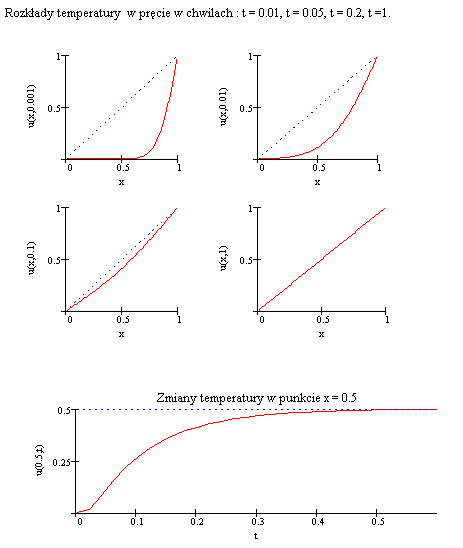
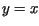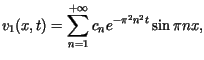
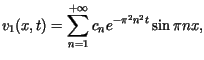
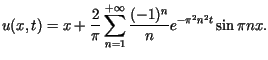
W miarę upływu czasu temperatura zbliża się do wartości funkcji liniowej we wszystkich punktach pręta.