



Next:Równanie
przewodnictwa cieplnego (I) Up:Metoda
Fouriera dla równańPrevious:Drgania
poprzeczne belkiSpis
rzeczy
Zadania
-
Rozwiązać równanie
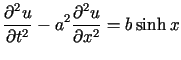 przy jednorodnych warunkach początkowych i brzegowych
przy jednorodnych warunkach początkowych i brzegowych
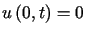 ,
, 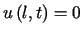 .
.
-
Rozwiązać równanie
 przy jednorodnych warunkach początkowych i brzegowych
przy jednorodnych warunkach początkowych i brzegowych
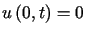 ,
, 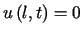 .
.
-
Rozwiązać równanie
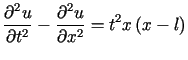 przy jednorodnych warunkach początkowych i brzegowych
przy jednorodnych warunkach początkowych i brzegowych
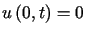 ,
, 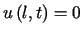 .
.
-
Rozwiązać równanie
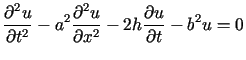 przy jednorodnych warunkach początkowych oraz przy warunkach brzegowych
przy jednorodnych warunkach początkowych oraz przy warunkach brzegowych
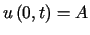 ,
, 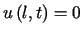 .
.
-
Rozwiązać równanie
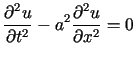 przy jednorodnych warunkach brzegowych
przy jednorodnych warunkach brzegowych
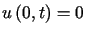 ,
, 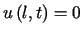 i warunkach początkowych
i warunkach początkowych
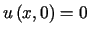 ,
, 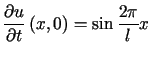 .
.
-
Rozwiązać równanie
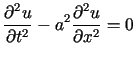 przy warunkach brzegowych
przy warunkach brzegowych
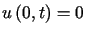 ,
, 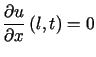 i warunkach początkowych
i warunkach początkowych
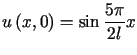 ,
, 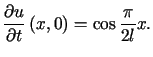
-
Rozwiązać równanie
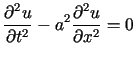 przy warunkach brzegowych
przy warunkach brzegowych
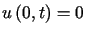 ,
, 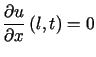 i warunkach początkowych
i warunkach początkowych
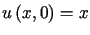 ,
, 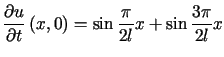 .
.
-
Rozwiązać równanie
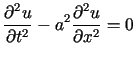 przy warunkach brzegowych
przy warunkach brzegowych
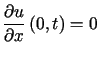 ,
, 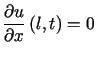 i warunkach początkowych
i warunkach początkowych
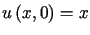 ,
, 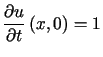 .
.
-
Rozwiązać równanie
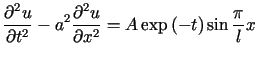 przy jednorodnych warunkach brzegowych
przy jednorodnych warunkach brzegowych
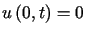 ,
, 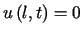 i jednorodnych warunkach początkowych
i jednorodnych warunkach początkowych
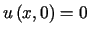 ,
, 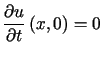 .
.
-
Rozwiązać równanie
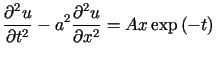 przy jednorodnych warunkach brzegowych
przy jednorodnych warunkach brzegowych
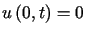 ,
, 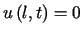 i jednorodnych warunkach początkowych
i jednorodnych warunkach początkowych
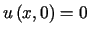 ,
, 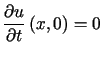 .
.
-
Rozwiązać równanie
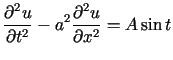 przy warunkach brzegowych
przy warunkach brzegowych
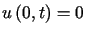 ,
, 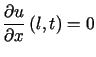 i jednorodnych warunkach początkowych
i jednorodnych warunkach początkowych
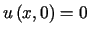 ,
, 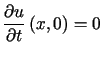 .
.
-
Rozwiązać równanie
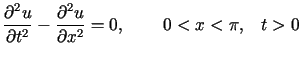 przy warunkach brzegowych
przy warunkach brzegowych
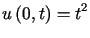 ,
, 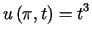 i warunkach początkowych
i warunkach początkowych
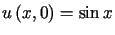 ,
, 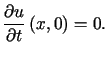
-
Rozwiązać równanie
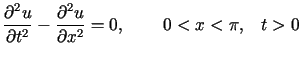 przy warunkach brzegowych
przy warunkach brzegowych
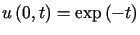 ,
, 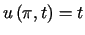 i warunkach początkowych
i warunkach początkowych
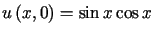 ,
, 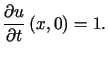
-
Rozwiązać równanie
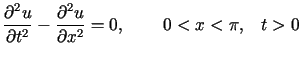 przy warunkach brzegowych
przy warunkach brzegowych
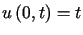 ,
, 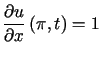 i warunkach początkowych
i warunkach początkowych
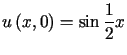 ,
, 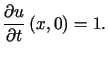
-
Rozwiązać równanie
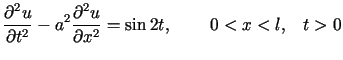 przy warunkach brzegowych
przy warunkach brzegowych
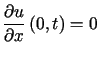 ,
, 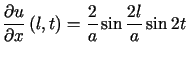 i warunkach początkowych
i warunkach początkowych
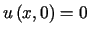 ,
, 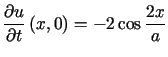 .
.




Next:Równanie
przewodnictwa cieplnego (I) Up:Metoda
Fouriera dla równańPrevious:Drgania
poprzeczne belkiSpis
rzeczy
Administrator 2003-01-27
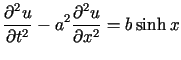

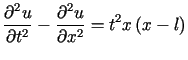
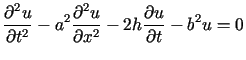
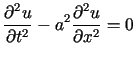
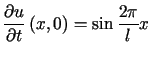 .
.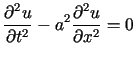
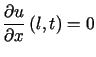
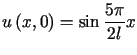 ,
, 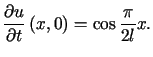
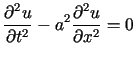
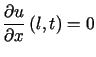
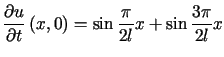 .
.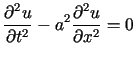
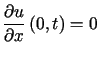 ,
, 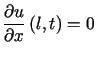
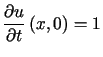 .
.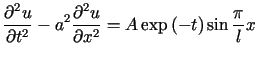
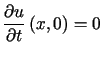 .
.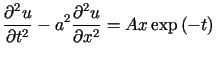
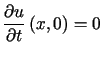 .
.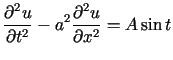
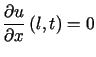
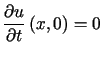 .
.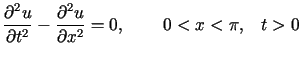
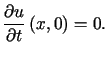
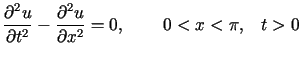
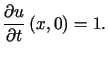
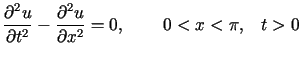
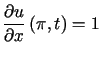
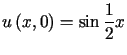 ,
, 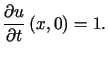
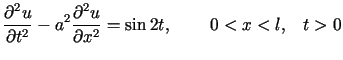
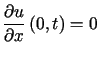 ,
, 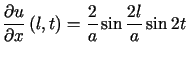
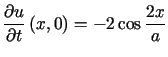 .
.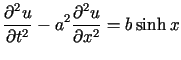

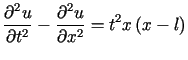
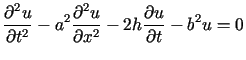
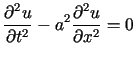
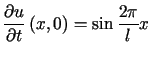 .
.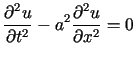
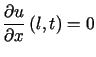
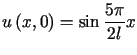 ,
, 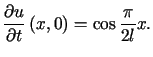
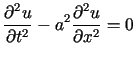
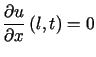
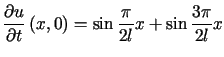 .
.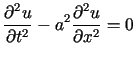
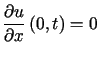 ,
, 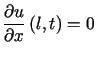
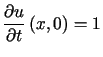 .
.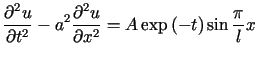
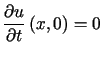 .
.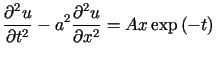
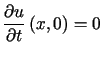 .
.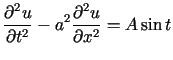
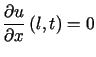
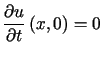 .
.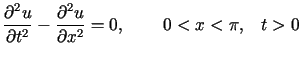
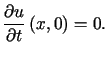
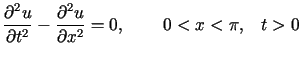
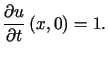
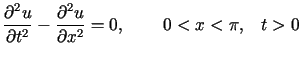
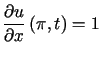
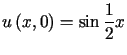 ,
, 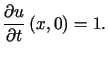
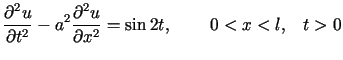
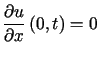 ,
, 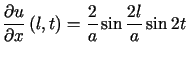
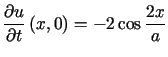 .
.