| (3.35) |
| (3.35) |
z warunkami początkowymi
| (3.36) |
opisującymi kształt początkowy belki i początkową prędkość drgań oraz warunkami brzegowymi postaci
| (3.37) |
Podobnie jak w przypadku struny, poszukujemy niezerowych rozwiązań równania
(3.35) spełniających jednocześnie warunki
brzegowe (3.37), w postaci ![]() .
Prowadzi to do problemu wyznaczenia wartości własnych
.
Prowadzi to do problemu wyznaczenia wartości własnych ![]() ,
dla których istnieją niezerowe funkcje
,
dla których istnieją niezerowe funkcje ![]() spełniające równanie
spełniające równanie
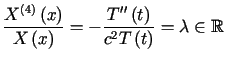 |
(3.38) |
z warunkami
| (3.39) |
Z rozważań analogicznych do przypadku omówionego dla struny jednowymiarowej
wynika, że jedynymi liczbami ![]() o tej własności są liczby
o tej własności są liczby
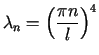 dla
dla ![$\displaystyle T_{n}\left( t\right)=A_{n}\sin\left[ c\left( \frac{\pi n}{l}\right) ^{2}t\right] +B_{n}%%\cos\left[ c\left( \frac{\pi n}{l}\right) ^{2}t\right]$](img532.gif) .
.![$\displaystyle u\left( x,t\right) =<tex2html_comment_mark>469 {\displaystyle\sum......left[ c\left( \frac{\pi n}{l}\right) ^{2}t\right] \right\} \sin\frac{\pi n}{l}x$](img533.gif) , , |
(3.40) |
gdzie współczynniki ![]() i
i ![]() szeregu (3.40) wyznaczamy z warunków początkowych
szeregu (3.40) wyznaczamy z warunków początkowych
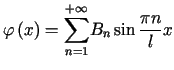 ,
, 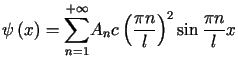 ,
,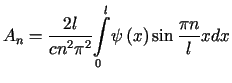 ,
, 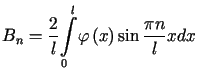 ,
dla
,
dla