



Next:Wstęp
do metod przybliżonychUp:Elementy
rachunku wariacyjnegoPrevious:Twierdzenie
o minimum funkcjonałuSpis
rzeczy
Zadania
W zadaniach 1-7 wyznaczyć ekstremale funkcjonałów zależnych od jednej funkcji,
przyjmując dowolne lecz ustalone warunki brzegowe.
-
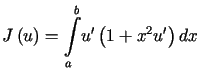
Odp.: 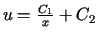
-
![$\displaystyle J\left( u\right) =%%{\displaystyle\int\limits_{a}^{b}}\left[ \left( u^{\prime}\right) ^{2}+2u^{\prime}u-16u^{2}\right] dx$](img1981.gif)
Odp.: 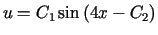
-
![$\displaystyle J\left( u\right) =%%{\displaystyle\int\limits_{a}^{b}}\left[ xu^{\prime}+\left( u^{\prime}\right) ^{2}\right] dx$](img1983.gif)
Odp.: 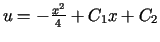
-
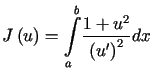
Odp.: 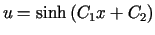
-
![$\displaystyle J\left( u\right) =%%{\displaystyle\int\limits_{a}^{b}}\left[ u^{2}+\left( u^{\prime}\right) ^{2}-2u\sin x\right] dx$](img1987.gif)
Odp.: 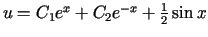
-
![$\displaystyle J\left( u\right) =%%{\displaystyle\int\limits_{a}^{b}}\left[ x^{2}\left( u^{\prime}\right) ^{2}+2u^{2}+2xu\right] dx$](img1989.gif)
Odp.: 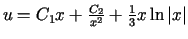
-
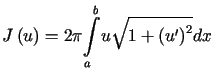
Odp.: 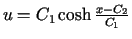
-
Wyznaczyć ekstremale funkcjonału zależnego od dwóch funkcji, przyjmując
dowolne lecz ustalone warunki brzegowe
![$\displaystyle J\left( u_{1},u_{2}\right) =%%{\displaystyle\int\limits_{a}^{b}}......+\left( u_{1}^{\prime}\right) ^{2}-\left(u_{2}^{\prime}\right) ^{2}\right] dx$](img1993.gif)
Odp.: 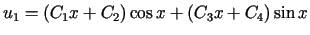
-
Wyznaczyć ekstremale funkcjonału zależnego od dwóch funkcji
![$\displaystyle J\left( u_{1},u_{2}\right) =%%{\displaystyle\int\limits_{0}^{\fr......\left( u_{1}^{\prime}\right) ^{2}+\left( u_{2}^{\prime}\right) ^{2}\right] dx$](img1995.gif) przyjmując warunki brzegowe:
przyjmując warunki brzegowe: 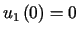 ,
, 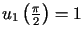 ,
, 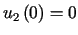 ,
, 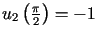 .
.
Odp.: 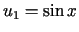 ,
, 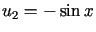
W zadaniach 10-12 wyznaczyć ekstremale funkcjonałów zależnych od jednej
funkcji, przyjmując dowolne lecz ustalone warunki brzegowe.
-
10.
-
![$\displaystyle J\left( u\right) =%%{\displaystyle\int\limits_{a}^{b}}\left[ \l......ime\prime}\right) ^{2}-2\left( u^{\prime}\right)^{2}+u^{2}-2u\sin x\right] dx$](img2002.gif)
Odp.: 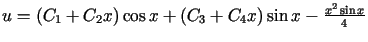
-
11.
-
![$\displaystyle J\left( u\right) =%%{\displaystyle\int\limits_{a}^{b}}\left[ \left( u^{\prime\prime\prime}\right) ^{2}+2xu\right] dx$](img2004.gif)
Odp.: 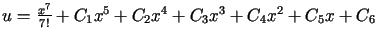
-
12.
-
![$\displaystyle J\left( u\right) =%%{\displaystyle\int\limits_{a}^{b}}\left[ \left( u^{\prime\prime\prime}\right) ^{2}+u^{2}-2x^{3}u\right] dx$](img2006.gif)
Odp.: 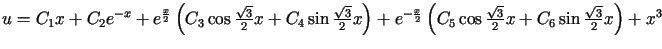
-
13.
-
Wyznaczyć ekstremale funkcjonału
![$\displaystyle J\left( u\right) =%%{\displaystyle\int\limits_{a}^{b}}\left[ \left( u^{\prime\prime}\right) ^{2}-u^{2}+x^{2}\right] dx$](img2008.gif) przyjmując warunki brzegowe:
przyjmując warunki brzegowe: 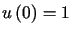 ,
, 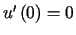 ,
, 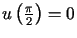 ,
, 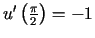 .
.
Odp.: 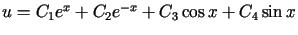




Next:Wstęp
do metod przybliżonychUp:Elementy
rachunku wariacyjnegoPrevious:Twierdzenie
o minimum funkcjonałuSpis
rzeczy
Administrator 2003-04-06
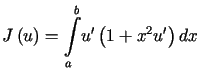
![$\displaystyle J\left( u\right) =%%{\displaystyle\int\limits_{a}^{b}}\left[ \left( u^{\prime}\right) ^{2}+2u^{\prime}u-16u^{2}\right] dx$](img1981.gif)
![$\displaystyle J\left( u\right) =%%{\displaystyle\int\limits_{a}^{b}}\left[ xu^{\prime}+\left( u^{\prime}\right) ^{2}\right] dx$](img1983.gif)
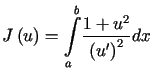
![$\displaystyle J\left( u\right) =%%{\displaystyle\int\limits_{a}^{b}}\left[ u^{2}+\left( u^{\prime}\right) ^{2}-2u\sin x\right] dx$](img1987.gif)
![$\displaystyle J\left( u\right) =%%{\displaystyle\int\limits_{a}^{b}}\left[ x^{2}\left( u^{\prime}\right) ^{2}+2u^{2}+2xu\right] dx$](img1989.gif)
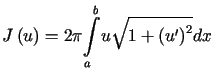
![$\displaystyle J\left( u_{1},u_{2}\right) =%%{\displaystyle\int\limits_{a}^{b}}......+\left( u_{1}^{\prime}\right) ^{2}-\left(u_{2}^{\prime}\right) ^{2}\right] dx$](img1993.gif)
![$\displaystyle J\left( u_{1},u_{2}\right) =%%{\displaystyle\int\limits_{0}^{\fr......\left( u_{1}^{\prime}\right) ^{2}+\left( u_{2}^{\prime}\right) ^{2}\right] dx$](img1995.gif) przyjmując warunki brzegowe:
przyjmując warunki brzegowe: 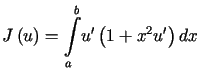
![$\displaystyle J\left( u\right) =%%{\displaystyle\int\limits_{a}^{b}}\left[ \left( u^{\prime}\right) ^{2}+2u^{\prime}u-16u^{2}\right] dx$](img1981.gif)
![$\displaystyle J\left( u\right) =%%{\displaystyle\int\limits_{a}^{b}}\left[ xu^{\prime}+\left( u^{\prime}\right) ^{2}\right] dx$](img1983.gif)
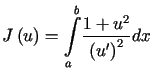
![$\displaystyle J\left( u\right) =%%{\displaystyle\int\limits_{a}^{b}}\left[ u^{2}+\left( u^{\prime}\right) ^{2}-2u\sin x\right] dx$](img1987.gif)
![$\displaystyle J\left( u\right) =%%{\displaystyle\int\limits_{a}^{b}}\left[ x^{2}\left( u^{\prime}\right) ^{2}+2u^{2}+2xu\right] dx$](img1989.gif)
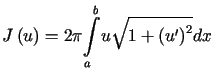
![$\displaystyle J\left( u_{1},u_{2}\right) =%%{\displaystyle\int\limits_{a}^{b}}......+\left( u_{1}^{\prime}\right) ^{2}-\left(u_{2}^{\prime}\right) ^{2}\right] dx$](img1993.gif)
![$\displaystyle J\left( u_{1},u_{2}\right) =%%{\displaystyle\int\limits_{0}^{\fr......\left( u_{1}^{\prime}\right) ^{2}+\left( u_{2}^{\prime}\right) ^{2}\right] dx$](img1995.gif) przyjmując warunki brzegowe:
przyjmując warunki brzegowe: ![$\displaystyle J\left( u\right) =%%{\displaystyle\int\limits_{a}^{b}}\left[ \l......ime\prime}\right) ^{2}-2\left( u^{\prime}\right)^{2}+u^{2}-2u\sin x\right] dx$](img2002.gif)
![$\displaystyle J\left( u\right) =%%{\displaystyle\int\limits_{a}^{b}}\left[ \left( u^{\prime\prime\prime}\right) ^{2}+2xu\right] dx$](img2004.gif)
![$\displaystyle J\left( u\right) =%%{\displaystyle\int\limits_{a}^{b}}\left[ \left( u^{\prime\prime\prime}\right) ^{2}+u^{2}-2x^{3}u\right] dx$](img2006.gif)
![$\displaystyle J\left( u\right) =%%{\displaystyle\int\limits_{a}^{b}}\left[ \left( u^{\prime\prime}\right) ^{2}-u^{2}+x^{2}\right] dx$](img2008.gif) przyjmując warunki brzegowe:
przyjmując warunki brzegowe: