Spis rzeczy

Twierdzenie o minimum funkcjonału kwadratowego

Z poprzednich rozważań wynika, że zagadnienia poszukiwania ekstremali funkcjonałów prowadzą do pewnych zagadnień brzegowych dla równań różniczkowych cząstkowych. Okazuje się, że również zagadnienia brzegowe dla równań różniczkowych związane są z wyznaczeniem ekstremów funkcjonałów.

Niech $H$ będzie pewną przestrzenią Hilberta, w której rozważane jest równanie

$$Au=f$$ (13.36)

gdzie  jest operatorem określonym na pewnej podprzestrzeni liniowej$D_{A}\subset H$ o wartościach w przestrzeni $H$. Zakładamy, że$\overline{D}_{A}=H$, tzn. $D_{A}$ jest gęsta w $H$. Załóżmy również, że  jest operatorem liniowym symetrycznym, tzn.

$$\left( Au,v\right) =\left( u,Av\right)%%$$ (13.37)

dla wszystkich $u,v\in D_{A}$, oraz dodatnim, tzn.

$$\left( Au,u\right) \geq0 \left( Au,u\right) =0\Longrightarrow u=0 u\in D_{A}$$ (13.38)

T w i er d z e n i e

Jeśli  jest dodatni w podprzestrzeni $D_{A}$, wówczas równanie$Au=f$, gdzie $f\in H$, posiada co najwyżej jedno rozwiązanie $u\inD_{A}\subset H$.

Dla dowodu wystarczy zauważyć, że gdyby elementy  i  były dwoma różnymi rozwiązaniami tego równania, to

$$0=Au_{1}-Au_{2}=A\left( u_{1}-u_{2}\right)$$ skąd wynika, że $$\left( A\left( u_{1}-u_{2}\right) ,u_{1}-u_{2}\right) =0\Longrightarrowu_{1}-u_{2}=0$$, a zatem $u_{1}=u_{2}$.

T w i e r d z e n i e (o minimum funkcjonału kwadratowego)

Niech  będzie symetryczny i dodatni w podprzestrzeni $D_{A}$, niech$f\in H$. Wówczas jeśli równanie $Au=f$ jest spełnione dla$u_{0}\in D_{A}$, tzn. $Au_{0}=f$, to funkcjonał

$$F\left( u\right) =\left( Au,u\right) -2\left( f,u\right)%%$$ (13.39)

osiąga swoją najmniejszą wartość w $D_{A}$ w punkcie $u=u_{0}$.
 

Dla dowodu konieczności warunku wystarczy zauważyć, że

$$F\left( u\right) =\left( Au,u\right) -2\left( f,u\right) =\left( Au,u\right) -2\left( Au_{0},u\right) =$$

$$=\left( Au,u\right) -\left( Au_{0},u\right) -\left( u,Au_{0}\right) =\left( Au,u\right) -\left( Au_{0},u\right) -\left( Au,u_{0}\right) =$$

$$=\left( A\left( u-u_{0}\right) ,u-u_{0}\right) -\left( Au_{0}<tex2html_comment_mark>2674 ,u_{0}\right)$$

Z warunku (13.38) wynika, że wartość $F\left( u\right)$ jest najmniejsza gdy $\left( A\left( u-u_{0}\right) ,u-u_{0}\right) =0$, tzn. gdy $u=u_{0}$.

Dla dowodu implikacji w stronę przeciwną rozważmy funkcję zmiennej $t\in\mathbb{R}$ określoną dla dowolnego $v\in D_{A}$ wzorem

$$F\left( u_{0}+tv\right) =\left( A\left( u_{0}+tv\right) ,u_{0}<tex2html_comment_mark>2676 +tv\right) -2\left( f,u_{0}+tv\right) =$$

$$=t^{2}\left( Av,v\right) +2t\left( Au_{0},v\right) -2t\left( f,v\right) +\left( Au_{0},u_{0}\right) -2\left( f,u_{0}\right)$$

Funkcja ta zgodnie z założeniem ma minimum lokalne w punkcie , zatem

$$\frac{d}{dt}F\left( u_{0}+tv\right) _{\vert t=0}=0$$ tzn. $$2\left( Au_{0},v\right) -2\left( f,v\right) =0\Longrightarrow\left(Au_{0}-f,v\right) =0$$ dla dowolnego $$v\in D_{A}$$. Na mocy gęstości podprzestrzeni $D_{A}$ wnioskujemy, że $Au_{0}=f$ w $H$.

P r z y k ł a d

Rozważmy równanie

$$\left( E\left( x\right) I\left( x\right) u^{\prime\prime}\left( x\right) \right) ^{\prime\prime}=q\left( x\right)%%$$ (13.40)

z warunkami

$$u\left( 0\right) =u\left( l\right) =0 u^{\prime}\left( 0\right) =u^{\prime}\left( l\right) =0$$ (13.41)

gdzie $E,I\in C^{2}\left( \left[ 0;l\right] \right)$, $q\in C\left(\left[ 0;l\right] \right)$ oraz $E\left( x>0\right)$, $I\left(x\right) >0$.

Równanie (13.40) opisuje ugięcie pręta o długości $l,$ module sprężystości $E\left( x\right)$, momencie bezwładności przekroju względem osi ugięcia $I\left( x\right)$, pod działaniem obciążenia $q\left( x\right)$. Warunki (13.41) oznaczają, że pręt jest zamocowany na końcach.

Niech $H=L^{2}\left( 0;l\right)$, $D_{A}$ - zbiór funkcji klasy $C^{4}$ spełniających warunki brzegowe (13.41), operator  zdefiniowany jest jako

$$A:D_{A}\rightarrow H$$, $$Au=\left( EIu^{\prime\prime}\right)^{\prime\prime}$$. Operator ten jest symetryczny, ponieważ na mocy wzoru o całkowaniu przez części otrzymujemy dla $u,v\in D_{A}$

$$\left( Au,v\right) =<tex2html_comment_mark>2687 {\displaystyle\int\limits_{0}^{l}} \......yle\int\limits_{0}^{l}} \left( EIu^{\prime\prime}\right) ^{\prime}v^{\prime}dx=$$

$$=-\underset{0}{\underbrace{\left. \left( EIu^{\prime\prime}\right......rk>2700 {\displaystyle\int\limits_{0}^{l}} EIu^{\prime\prime}v^{\prime\prime}dx$$

Analogicznie łatwo przeliczyć, że

$$\left( u,Av\right) =%%{\displaystyle\int\limits_{0}^{l}}EIu^{\prime\prime}v^{\prime\prime}dx$$, zatem $\left( Au,v\right) =\left( u,Av\right)$ dla dowolnych $u,v\in D_{A}$.

Ponadto

$$\left( Au,u\right) =%%{\displaystyle\int\limits_{0}^{l}}EI\left( u^{\prime\prime}\right) ^{2}dx\geq0$$ oraz z równości $\left( Au,u\right) =0$ wynika, że$u^{\prime\prime}\equiv0$, a więc $u\left( x\right) =ax+b$. Ponieważ każda funkcja  należąca do podprzestrzeni $D_{A}$ spelnia jednorodne warunki brzegowe (13.41), więc . Oznacza to, że operator  jest dodatni.

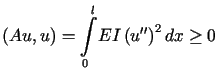
Funkcjonał  jest w tym przypadku postaci

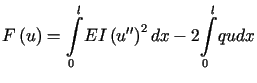$$F\left( u\right) =<tex2html_comment_mark>2714 {\displaystyle\int\......eft( u^{\prime\prime}\right) ^{2}dx-2{\displaystyle\int\limits_{0}^{l}} qudx%%$$ (13.42)

i wyraża dla danego ugięcia podwojoną energię potencjalną pręta.

Jeśli $u_{0}$ jest rozwiązaniem problemu, to rozumując podobnie jak w dowodzie twierdzenia o minimum funkcjonału kwadratowego, łatwo pokazać, że

$$F\left( u\right) =%%{\displaystyle\int\limits_{0}^{l}}EI\left( ......{\displaystyle\int\limits_{0}^{l}}EI\left( u_{0}^{\prime\prime}\right) ^{2}dx$$.

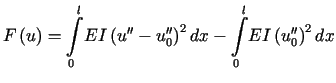U w a g a

Twierdzenie o minimum funkcjonału kwadratowego transformuje problem znalezienia rozwiązania równania $Au=f$ do problemu znalezienia elementu $u_{0}\in D_{A}$ minimalizującego funkcjonał $F\left( u\right)$ na $D_{A}$. Twierdzenie to ma charakter warunkowy, tzn. nie gwarantuje a priori istnienia takiego elementu w danej podprzestrzeni $D_{A}$. W przypadku, gdy $F\left( u\right)$ nie przyjmuje najmniejszej wartości na $D_{A}$, zbiór $D_{A}$ wymaga rozszerzenia. Tą drogą można skonstruować definicję słabego rozwiązania rozważanego zagadnienia brzegowego, równoważną definicji słabego rozwiązania w przestrzeniach Sobolewa $H^{k}\left( \Omega\right)$.