Najstarsze fraktale

Opowiemy Wam o fraktalach, które wymyślili matematycy na początku XX-wieku. Te dziwne i ciekawe zarazem zbiory dały początek nowej geometrii zwanej geometrią fraktalną, która pozwala modelować wiele obiektów i zjawisk występujących w przyrodzie i nie tylko...

Co to jest fraktal ?

Naszą intencją nie jest podawanie formalnych definicji fraktali, ponieważ jest ich bardzo wiele. Wymienimy jedynie niektóre ich własności:

• Fraktal to zbiór o skomplikowanej budowie. Niezależnie od tego jak mały jego fragment będziemy oglądać - będzie on równie skomplikowany jak całość.
• Wiele fraktali kryje w sobie zadziwiającą tajemnicę jaką jest ich 'nieskończone samopodobieństwo'. Oznacza to, że dowolnie mały jego kawałek, odpowiednio powiększony, przypomina do złudzenia cały zbiór lub jego znaczną część.
• Jednocześnie fraktale mają prosty opis i często są otrzymywane przez powtarzanie nieskończenie wiele razy tej samej operacji. Jeśli przeczytacie opisy konstrukcji fraktali, które widać na ekranie, zrozumiecie co chcieliśmy powiedzieć.

Poniżej widać rysunki (tylko w przybliżeniu!) kilku fraktali. Aby dowiedzieć się o każdym z nich dlaczego jest fraktalem i jakie ma ciekawe własności wystarczy 'kliknąć' w miejscu jego nazwy.

[ Płatek śniegu ] [ Dywan Sierpińskiego ] [ Trójkąt Sierpińskiego ] [ Piramida Sierpińskiego ]

Wymiar Intuicja podpowiada nam, że odcinek lub okrąg powinny mieć wymiar równy 1, natomiast kwadrat lub brzeg sześciennej kostki powinny mieć wymiar 2, a sama kostka powinna być wymiaru 3. Wymyślenie dobrej definicji wymiaru było jednak bardzo trudne i wielu matematyków w początku XX wieku zmagało się z tym problemem. W kolejnych wykładach z cyklu Świat fraktali opowiemy o bardzo 'dziwnym' wymiarze zw. 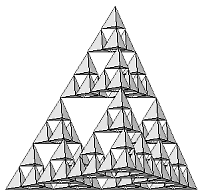wymiarem Minkowskiego i policzymy ile on wynosi dla zbiorów wymienionych wyżej oraz dla fraktali widocznych obok. Okaże się, że odcinek lub kwadrat mają wymiar Minkowskiego zgodny z nasza intuicją. Jednak dla fraktali może on przyjmować wartości, które jej przeczą np. dywan Sierpińskiego ma wymiar równy 1.5849..... Trudno w to uwierzyć a jednak tak jest! Opowiemy Wam jak 'narodził się' wymiar Minkowskiego. Wyjaśnimy gdzie i dlaczego należy z niego korzystać, oraz jaki ma on związek z innymi definicjami wymiaru, które być może już poznaliście.

Fraktale z naszej kolekcji to przykłady zbiorów o zdumiewających, trudnych do wyobrażenia własnościach, które wręcz przeczą naszej intuicji. Popatrzcie na brzeg 'płatka śniegu'. Chyba każdy z Was powie o nim, że jest krzywą. Czy powiedzielibyście to samo o dywanie Sierpińskiego? Choć brzmi to może absurdalnie, dywan jest także krzywą ale o bardzo skomplikowanej budowie.

Opisywane fraktale powstały na początku XX wieku w wyniku zmagań matematyków z definicją 'wymiaru' i 'krzywej'. Zbiory te kryją w sobie do dziś jeszcze nie rozwiązane zagadki.

Zachęcamy Was abyście zaglądali do naszych wykładów, bo dowiecie się o wielu ciekawostkach, które na pewno Was zaskoczą.

Krzywa W kolejnych wykładach opowiemy Wam jak matematycy odkrywali coraz to bardziej skomplikowane krzywe. W szczególności uzasadnimy dlaczego np. dywan Sierpińskiego jest krzywą. Dziś niektóre z tych bardzo 'dziwnych' krzywych znalazły ciekawe zastosowania, o których także Wam opowiemy.

[ Początek strony ] [ MiNIWyklady ]

---

Wszystkie prawa zastrzeżone © 2000 Wydział Matematyki i Nauk Informacyjnych Politechniki Warszawskiej