Znaleźć funkcję ![]() spełniającą równanie
spełniającą równanie
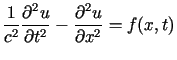 dla
dla |
(3.1) |
wraz z warunkami brzegowymi
| (3.2) |
i warunkami początkowymi
| (3.3) |
Zakładamy, że ![]() jest klasy
jest klasy ![]() ,
, ![]() ,
, ![]() ,
, ![]() są klasy
są klasy ![]() .
Zakładamy ponadto, że spełnione są tzw. warunki zgodności, tzn.
.
Zakładamy ponadto, że spełnione są tzw. warunki zgodności, tzn. ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Zagadnienie (3.1)-(3.3) rozwiążemy w kilku etapach, stosując tzw. metodę Fouriera zwaną także metodą separacji zmiennych.
| (3.4) |
oraz ![]() (brak siły zewnętrznej wymuszającej ruch).
(brak siły zewnętrznej wymuszającej ruch).
Najpierw rozwiążemy pewne zagadnienie pomocnicze.
Znaleźć rozwiązanie równania (3.1)
nie równe tożsamościowo zeru, spełniające warunki brzegowe (3.4)
i przedstawialne w postaci![]() ,
gdzie
funkcje
,
gdzie
funkcje![]() i
i ![]() zależą
tylko od jednej zmiennej.
zależą
tylko od jednej zmiennej.
Podstawiając ![]() do równania (3.1), gdzie
do równania (3.1), gdzie ![]() ,
otrzymujemy
,
otrzymujemy
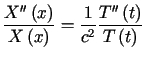 . . |
(3.5) |
Ponieważ równość (3.5) zachodzić musi
dla wszystkich![]() i
i ![]() z rozważanego zakresu, więc obie strony tej równości muszą być stałe. Oznaczając
tę stałą przez
z rozważanego zakresu, więc obie strony tej równości muszą być stałe. Oznaczając
tę stałą przez ![]() dostajemy równość
dostajemy równość
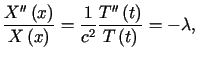
| (3.6) | ||
| (3.7) |
Z warunków brzegowych (3.4) wynika, że ![]() (w przeciwnym razie
(w przeciwnym razie ![]() i
i![]() ).
).
Dla funkcji ![]() otrzymaliśmy tzw. zagadnienie Sturma-Liouville'a polegające na wyznaczeniu
takich wartości
otrzymaliśmy tzw. zagadnienie Sturma-Liouville'a polegające na wyznaczeniu
takich wartości![]() ,
zwanych wartościami własnymi, przy których istnieją niezerowe rozwiązania
równania (3.6), zwane funkcjami własnymi,
spełniające warunki
,
zwanych wartościami własnymi, przy których istnieją niezerowe rozwiązania
równania (3.6), zwane funkcjami własnymi,
spełniające warunki ![]() .
.
W celu wyznaczenia wartości własnych zagadnienia należy rozważyć trzy następujące przypadki.
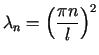 dla
dla |
(3.8) |
istnieją niezerowe funkcje
| (3.9) |
będące rozwiązaniami równania (3.6) z
warunkami![]() .
Liczby
.
Liczby ![]() są wartościami własnymi rozważanego zagadnienia.
są wartościami własnymi rozważanego zagadnienia.
| (3.10) |
W takim razie rozwiązaniem zagadnienia pomocniczego (3.1), (3.4) są funkcje
| (3.11) |
Aby skonstruować rozwiązanie spełniające także zadane warunki początkowe (3.3) tworzymy szereg
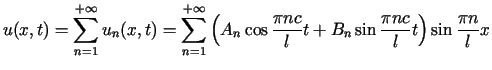 , , |
(3.12) |
którego współczynniki, zgodnie z teorią szeregów Fouriera, określone są wzorami
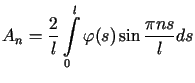 , , 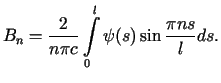 |
(3.13) |
T w i e r d z e n i e
Jeżeli ![]() jest klasy
jest klasy ![]() ,
,![]() ,
, ![]() jest klasy
jest klasy ![]() ,
, ![]() ,
to szereg (3.12) ze współczynnikami określonymi
wzorami (3.13) jest rozwiązaniem zagadnienia
(3.1) dla
,
to szereg (3.12) ze współczynnikami określonymi
wzorami (3.13) jest rozwiązaniem zagadnienia
(3.1) dla ![]() ,
z warunkami (3.3)-(3.4).
,
z warunkami (3.3)-(3.4).
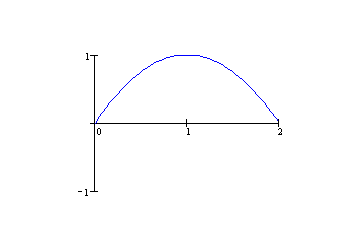
P r z y k ł a d 1
Rozwiązać omówione powyżej zagadnienie dla ![]()
![]()
![]() .
.
Ze wzorów (3.13) wynika, że
![$\displaystyle A_{n}=\frac{16}{n^{3}\pi^{3}}\left[ 1-(-1)^{n}\right] ,$](img397.gif)
![$\displaystyle u(x,t)=\frac{16}{\pi^{3}}\sum\limits_{n=1}^{+\infty}\frac{\left[1-(-1)^{n}\right] }{n^{3}}\sin\pi\frac{nx}{2}\cos\pi\frac{nt}{2}.$](img399.gif)
P r z y k ł a d 2
Rozwiązać omówione powyżej zagadnienie dla ![]()
![]() ,
,![]()
![]() .
.
Z podanych wzorów wynika, że
![$\displaystyle A_{n}=\frac{32}{n^{3}\pi^{3}}\left[ 2(-1)^{n+1}-1\right] ,$](img404.gif)
![$\displaystyle u(x,t)=\frac{32}{\pi^{3}}\sum\limits_{n=1}^{+\infty}\frac{\left[2(-1)^{n+1}-1\right] }{n^{3}}\sin\pi\frac{nx}{2}\cos\pi\frac{nt}{2}.$](img406.gif)
Wystarczy zatem wyznaczyć funkcję ![]() spełniającą równanie
spełniającą równanie
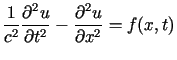 dla
dla |
(3.14) |
z warunkami
| (3.15) | ||
| (3.16) |
W tym celu załóżmy, że funkcja dana ![]() dla
dla![]() może być zapisana w postaci sinusowego szeregu Fouriera względem zmiennej
może być zapisana w postaci sinusowego szeregu Fouriera względem zmiennej ![]()
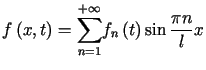 , , |
(3.17) |
gdzie
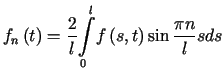 dla
dla 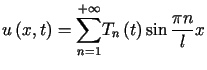 , , |
(3.18) |
gdzie ![]() są niewiadomymi funkcjami. Zakładając, że dozwolone jest różniczkowanie
szeregu (3.18) wyraz po wyrazie, z równania
(3.14) i przedstawienia (3.17)
otrzymujemy
są niewiadomymi funkcjami. Zakładając, że dozwolone jest różniczkowanie
szeregu (3.18) wyraz po wyrazie, z równania
(3.14) i przedstawienia (3.17)
otrzymujemy
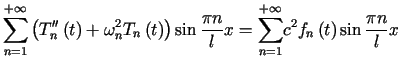 ,
,| (3.19) |
Z warunków (3.15) wynika ponadto, że
| (3.20) |
Rozwiązanie zagadnienia (3.19)-(3.20) można przedstawić w postaci
![$\displaystyle T_{n}\left( t\right) =\frac{2c}{\pi n}<tex2html_comment_mark>390 ......ft( s,r\right) \sin\frac{\pi n}{l}sds\right] \sin\omega_{n}\left( t-r\right) dr$](img424.gif) dla
dla |
(3.21) |
T w i e r d z e n i e
Jeżeli funkcja ![]() jest klasy
jest klasy ![]() oraz
oraz ![]() dla każdego
dla każdego ![]() ,
to szereg (3.18) ze współczynnikami określonymi
wzorami (3.21) jest rozwiązaniem zagadnienia
(3.14)-(3.16).
,
to szereg (3.18) ze współczynnikami określonymi
wzorami (3.21) jest rozwiązaniem zagadnienia
(3.14)-(3.16).
| (3.22) |
i poszukujemy rozwiązania zagadnienia w postaci ![]() .
.
Ponieważ ze wzoru (3.22) wynika, że ![]() i
i ![]() ,
więc
,
więc ![]() ,
tzn. funkcja
,
tzn. funkcja![]() jest rozwiązaniem pewnego zagadnienia postaci (3.1),
(3.3), (3.4)
z jednorodnymi warunkami brzegowymi. Zagadnienie wyznaczenia takiej funkcji
jest rozwiązaniem pewnego zagadnienia postaci (3.1),
(3.3), (3.4)
z jednorodnymi warunkami brzegowymi. Zagadnienie wyznaczenia takiej funkcji![]() zostało omówione w poprzednim punkcie.
zostało omówione w poprzednim punkcie.