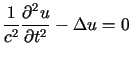 ,
gdzie ,
gdzie 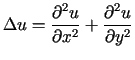 |
(3.23) |
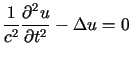 ,
gdzie ,
gdzie 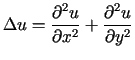 |
(3.23) |
rozważane dla ![]() ,
, ![]() .
Załóżmy,
że spełnione są warunki początkowe
.
Załóżmy,
że spełnione są warunki początkowe
| (3.24) |
oraz, że ![]() jest klasy
jest klasy ![]() ,
, ![]() jest klasy
jest klasy ![]() .
.
| (3.25) |
W celu rozwiązania tego zagadnienia postępujemy analogicznie jak w przypadku drgań swobodnych struny zamocowanej. Stosując metodę separacji zmiennych w postaci
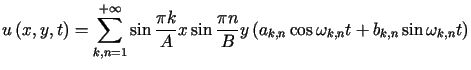 , , |
(3.26) |
gdzie
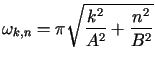 dla
dla
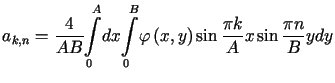 , , |
(3.27) | |
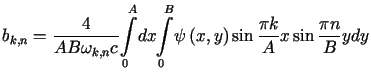 . . |
(3.28) |
P r z y k ł a d
Rozwiązać zagadnienie drgań membrany prostokątnej dla ![]()
![]()
![]()
![]() .
.
Zgodnie ze wzorami (3.27), (3.28),
całkując przez części wyznaczamy współczynniki ![]() i
i ![]()
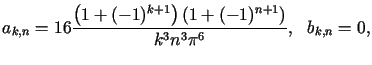
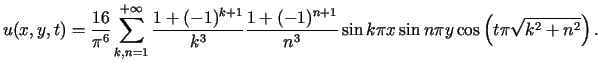
Plan warstwicowy w formacie avi (309 KB)
Plan warstwicowy - animowany
gif (164 KB)
| (3.29) |
Załóżmy, że funkcje ![]() i
i ![]() opisujące warunki początkowe (3.24) spełniają
zależność
opisujące warunki początkowe (3.24) spełniają
zależność
| (3.30) |
tzn. warunki te są kołowo symetryczne. O funkcjach danych załóżmy, że ![]() jest klasy
jest klasy ![]() pochodna
pochodna ![]() istnieje i jest przedziałami ciągła,
istnieje i jest przedziałami ciągła, ![]() ,
,![]() jest
klasy
jest
klasy ![]() ,
pochodna
,
pochodna ![]() istnieje
i jest przedziałami ciągła,
istnieje
i jest przedziałami ciągła, ![]()
Z symetrii równania i warunków wynika, że rozwiązanie ![]() może być poszukiwane w postaci
może być poszukiwane w postaci ![]() Przechodząc do współrzędnych biegunowych
Przechodząc do współrzędnych biegunowych ![]() ,
przekształcamy wyjściowe równanie do postaci (przyjmujemy, że
,
przekształcamy wyjściowe równanie do postaci (przyjmujemy, że ![]() nie zależy od
nie zależy od ![]() )
)
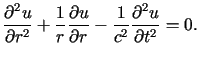 |
(3.31) |
Stosując metodę Fouriera (separacji zmiennych) dla ![]() otrzymujemy dwa równania
otrzymujemy dwa równania
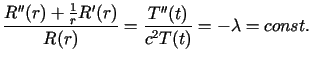
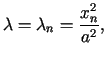 dla
dla Funkcje Bessela ![]() określone są wzorem
określone są wzorem
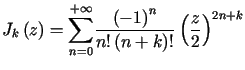 ,
,
W takim razie funkcja
![$\displaystyle u_{n}(x,t)=J_{0}\left( x_{n}\frac{r}{a}\right) \left[ A_{n}\cos\left( x_{n}\frac{ct}{a}\right) +B_{n}\sin\left( x_{n}\frac{ct}{a}\right) \right]$](img486.gif) dla
dla |
(3.32) |
i dowolnych stałych ![]() ,
, ![]() jest rozwiązaniem rozważanego równania (3.31)
spełniającym jednocześnie warunek brzegowy (3.29).
jest rozwiązaniem rozważanego równania (3.31)
spełniającym jednocześnie warunek brzegowy (3.29).
Pełnym rozwiązaniem zagadnienia, spełniającym także warunki początkowe
(3.30), jest funkcja ![]() określona jako suma szeregu
określona jako suma szeregu
![$\displaystyle u(r,t)=\sum\limits_{n=1}^{+\infty}J_{0}\left( x_{n}\frac{r}{a}\ri......( x_{n}\frac{ct}{a}\right) +B_{n}\sin\left( x_{n}\frac{ct}{a}\right) \right]%%$](img491.gif) |
(3.33) |
gdzie stałe![]() i
i ![]() wyznaczone są za pomocą wzorów
wyznaczone są za pomocą wzorów
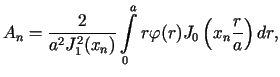 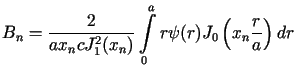 |
(3.34) |
dla ![]() ,
, ![]() .
.
P r z y k ł a d
Rozwiązać zagadnienie drgań membrany kołowej dla ![]()
![]()
![]()
Z danych zadania wynika, że
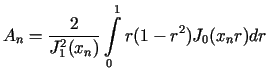 dla
dla ![$\displaystyle \frac{d}{dx}\left[ x^{n}J_{n}(x)\right] =x^{n}J_{n-1}(x)$](img501.gif)
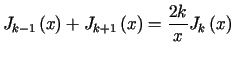
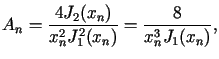
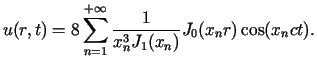
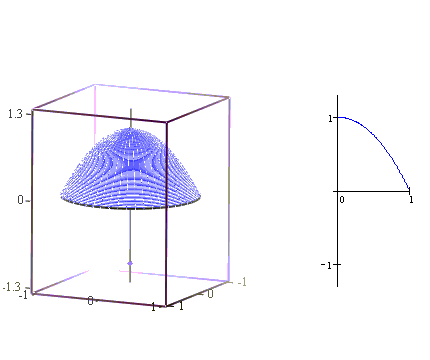
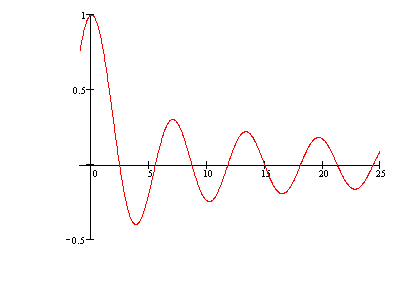
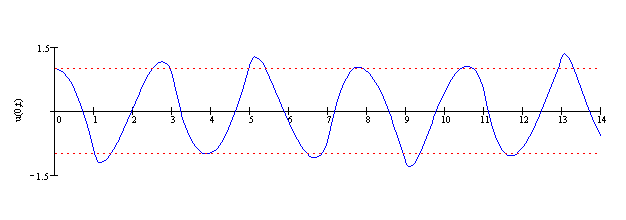
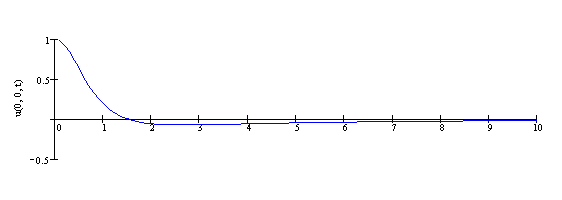
Kolejny rysunek przedstawia drgania punktu położonego na osi symetrii
membrany jako funkcję zmiennej ![]() .
.
Plan warstwicowy w formacie avi (285 KB)
Plan warstwicowy - animowany
gif (175 KB)
Następujące twierdzenie określa warunki dostateczne dla istnienia rozwiązania
i podaje jego postać (tzw. wzór Poissona).
T w i e r d z e n i e
Jeżeli funkcje ![]() i
i ![]() są odpowiednio klasy
są odpowiednio klasy ![]() i
i![]() ,
to funkcja
,
to funkcja ![]() postaci
postaci
![$\displaystyle u(x,y,t)=\frac{1}{2\pi c}\iint\limits_{K_{ct}}\frac{\psi(p,q)dpdq......_{ct}}\frac{\varphi(p,q)dpdq}{\sqrt{c^{2}%%t^{2}-(p-x)^{2}-(q-y)^{2}}}\right]$](img507.gif)
P r z y k ł a d
Rozwiązać zagadnienie drgań membrany nieograniczonej dla danych:
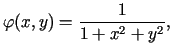
![$\displaystyle =\frac{\partial}{\partial t}\left[ \frac{1}{2\pi}\int \limits_{0}......phi(x+r\cos\alpha,y+r\sin\alpha )\frac{r}{\sqrt{t^{2}-r^{2}}}drd\alpha\right] =$](img517.gif) |
||
![$\displaystyle =\frac{\partial}{\partial t}\left[ \frac{1}{2\pi}\int\limits_{0}^......r^{2}+2xr\cos\alpha+2yr\sin\alpha }\frac{r}{\sqrt{t^{2}-r^{2}}}drd\alpha\right]$](img518.gif) |
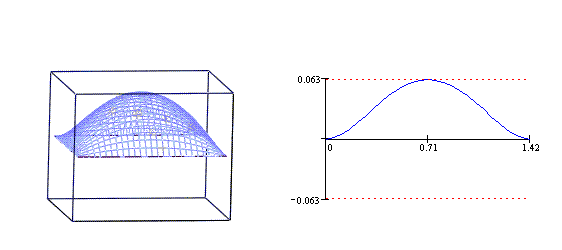
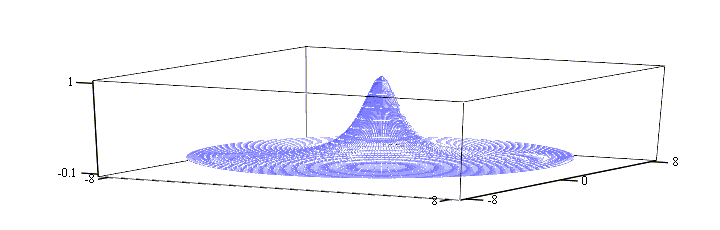
Poniższy rysunek przedstawia wygląd membrany w chwili ![]() .
.
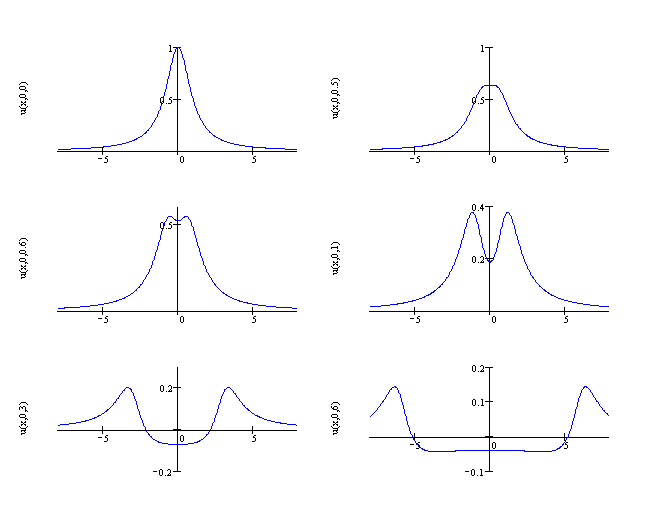
Na następnym rysunku widoczne są kształty przekrojów osiowych membrany
dla ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
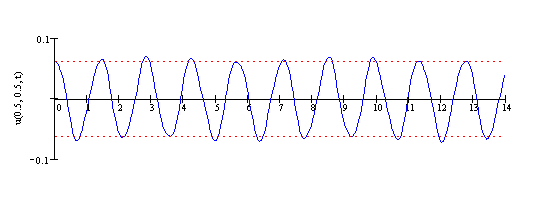
Kolejny rysunek przedstawia drgania punktu położonego na osi symetrii
membrany jako funkcję zmiennej ![]() .
.
Plan warstwicowy w formacie avi (338 KB)
Plan warstwicowy - animowany
gif (204 KB)