| (4.1) |
| (4.1) |
Funkcja ![]() przedstawia temperaturę pręta w punkcie
przedstawia temperaturę pręta w punkcie ![]() ,
w chwili czasu
,
w chwili czasu ![]() .
.
Zakładamy, że dany jest początkowy rozkład temperatury
| (4.2) |
gdzie ![]() jest funkcja daną.
jest funkcja daną.
Zagadnienie polegajace na znalezieniu rozwiązania równania (4.1) spełniającego warunek (4.2) nazywamy zagadnieniem Cauchy'ego (zagadnieniem początkowym) dla równania przewodnictwa.
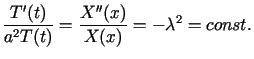
| (4.3) |
spełnia równanie (4.1) - być może bez
zadanego warunku początkowego (4.2). Wyrażenia ![]() i
i![]() są w tym momencie dowolnymi funkcjami zmiennej
są w tym momencie dowolnymi funkcjami zmiennej ![]() .
.
Zastosujemy teraz następujące twierdzenie pomocnicze.
T w i e r d z e n i e
Jeżeli funkcja ![]() dla każdej wartości rzeczywistej parametru
dla każdej wartości rzeczywistej parametru ![]() spełnia względem zmiennych
spełnia względem zmiennych ![]() liniowe równanie różniczkowe
liniowe równanie różniczkowe ![]() ,
to całka postaci
,
to całka postaci
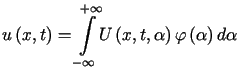 |
(4.4) |
jest także rozwiązaniem tego równania, o ile można obliczyć pochodne
występujące w równaniu ![]() przez różniczkowanie pod znakiem całki.
przez różniczkowanie pod znakiem całki.
Stosując powyższe twierdzenie do funkcji ![]() przedstawiamy rozwiązanie zagadnienia Cauchy'ego w postaci
przedstawiamy rozwiązanie zagadnienia Cauchy'ego w postaci
![$\displaystyle u(x,t)=\int\limits_{-\infty}^{+\infty}\exp\left( -a^{2}\lambda^{2}t\right) \left[ A(\lambda)\cos\lambda x+B(\lambda)\sin\lambda x\right] d\lambda$](img598.gif) . . |
(4.5) |
Podstawiając ![]() i uwzględniając warunek początkowy (4.2)
otrzymujemy
i uwzględniając warunek początkowy (4.2)
otrzymujemy
![$\displaystyle \varphi\left( x\right) =u\left( x,0\right) =\int\limits_{-\infty}......{+\infty}\left[ A(\lambda)\cos\lambda x+B(\lambda)\sin\lambda x\right] d\lambda$](img599.gif) . . |
(4.6) |
Z równości (4.6) należy wyznaczyć niewiadome
funkcje![]() i
i ![]() .
.
Zadanie to jest równoważne przedstawieniu danej funkcji ![]() w postaci tzw. całki Fouriera. Korzystając z teorii szeregów Fouriera,
dowodzi się prawdziwości następującego twierdzenia.
w postaci tzw. całki Fouriera. Korzystając z teorii szeregów Fouriera,
dowodzi się prawdziwości następującego twierdzenia.
T w i e r d z e n i e
Jeżeli funkcja ![]() jest sumą swojego szeregu Fouriera w każdym przedziale postaci
jest sumą swojego szeregu Fouriera w każdym przedziale postaci ![]() oraz jest bezwzględnie całkowalna na osi rzeczywistej, tzn. zbieżna jest
całka niewłaściwa
oraz jest bezwzględnie całkowalna na osi rzeczywistej, tzn. zbieżna jest
całka niewłaściwa 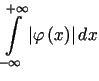 ,
to funkcję
,
to funkcję ![]() przedstawić można w postaci całki Fouriera
przedstawić można w postaci całki Fouriera
![$\displaystyle \varphi\left( x\right) =\int\limits_{-\infty}^{+\infty}\left[ A(\lambda)\cos\lambda x+B(\lambda)\sin\lambda x\right] d\lambda$](img604.gif) , , |
(4.7) |
gdzie
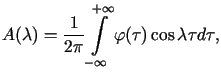 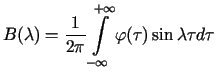 . . |
(4.8) |
Z powyższego twierdzenia wynika bezpośrednio, że wzór (4.5),
w którym funkcje ![]() i
i ![]() określone są wzorami (4.8) przedstawia rozwiązanie
zagadnienia Cauchy'ego (4.1)-(4.2).
określone są wzorami (4.8) przedstawia rozwiązanie
zagadnienia Cauchy'ego (4.1)-(4.2).
L e m a t
Zachodzi tożsamość
![$\displaystyle <tex2html_comment_mark>570 {\displaystyle\int\limits_{0}^{+\infty......sqrt{\pi}}{2a\sqrt{t}}\exp\left[ -\frac{\left( t-x\right) ^{2}}{4a^{2}t}\right]$](img607.gif) . . |
(4.9) |
Dla dowodu wzoru, przekształcamy całkę po lewej stronie równości (4.9) jak następuje.
![$\displaystyle <tex2html_comment_mark>576 {\displaystyle\int\limits_{0}^{+\infty......2 {\displaystyle\int\limits_{0}^{+\infty}} \exp\left[ -z^{2}\right] \cos\mu zdz$](img608.gif) . . |
(4.10) |
Oznaczmy ![$ \Phi\left( \mu\right) =%%{\displaystyle\int\limits_{0}^{+\infty}}\exp\left[ -z^{2}\right] \cos\mu zdz$](img609.gif) .
Wtedy
.
Wtedy
![$\displaystyle \Phi^{\prime}\left( \mu\right) =-%%{\displaystyle\int\limits_{0}......nfty}}\exp\left[ -z^{2}\right] \cos\mu zdz=-\frac{\mu}{2}\Phi\left( \mu\right)$](img610.gif) .
.Ponieważ ![]() ,
więc
,
więc
![$\displaystyle C=%%{\displaystyle\int\limits_{0}^{+\infty}}\exp\left[ -z^{2}\right] dz=\frac{\sqrt{\pi}}{2}$](img614.gif) .
.![$\displaystyle %%{\displaystyle\int\limits_{0}^{+\infty}}\exp\left[ -a^{2}\lam......t{\pi}}%%{2a\sqrt{t}}\exp\left[ -\frac{\left( t-x\right) ^{2}}{4a^{2}t}\right]$](img616.gif) ,
,Podstawiając wzory (4.8) do (4.5) i stosując pewne elementarne wzory trygonometryczne otrzymujemy
![$\displaystyle u(x,t)=\frac{1}{\pi}\int\limits_{0}^{+\infty}\left[{\displaystyl......a^{2}\lambda^{2}t\right) \cos\lambda\left( \tau-x\right) d\tau\right] d\lambda$](img617.gif) .
.![$\displaystyle =\frac{1}{\pi}\int\limits_{-\infty}^{+\infty}\left[ {\displaystyl......cos\lambda\left( \tau-x\right) d\lambda\right] \varphi\left( \tau\right) d\tau=$](img619.gif) |
||
![$\displaystyle =\frac{1}{2a\sqrt{\pi t}}<tex2html_comment_mark>624 {\displaystyl......rac{\left( \tau-x\right) ^{2}<tex2html_comment_mark>628 }{4a^{2}t}\right] d\tau$](img620.gif) . . |
(4.11) |
Wprowadzając oznaczenie
![$\displaystyle F\left( x,t,\tau\right) =\frac{1}{2a\sqrt{\pi t}}\exp\left[ -\frac{\left( \tau-x\right) ^{2}}{4a^{2}t}\right]%%$](img621.gif) |
(4.12) |
możemy wzór (4.11) zapisać w prostszej postaci
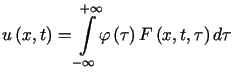 . . |
(4.13) |
Funkcję ![]() określoną wzorem (4.12) nazywamy rozwiązaniem
podstawowym równania przewodnictwa cieplnego, zaś wzór (4.13)
opisujący rozwiązanie zagadnienia Cauchy'ego - całką Poissona.
określoną wzorem (4.12) nazywamy rozwiązaniem
podstawowym równania przewodnictwa cieplnego, zaś wzór (4.13)
opisujący rozwiązanie zagadnienia Cauchy'ego - całką Poissona.
P r z y k ł a d 1
Rozwiązać powyższe zagadnienie początkowe (4.1)-(4.2)
dla ![]() oraz
oraz ![]() określonej wzorem
określonej wzorem
![\begin{displaymath}\varphi(x)=\left\{\begin{array}[c]{ll}%%3 & \text{dla }\le......0 & \text{dla }\left\vert x\right\vert >1.\end{array}\right.\end{displaymath}](img626.gif)
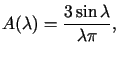
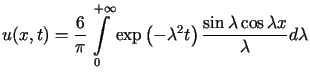
![$\displaystyle u(x,t)=\frac{3}{2\sqrt{\pi t}}\int\limits_{-1}^{+1}\exp\left[ -\frac{\left(\tau-x\right) ^{2}}{4t}\right] d\tau\text{.}%%$](img630.gif)
P r z y k ł a d 2
Rozwiązać powyższe zagadnienie początkowe dla ![]() oraz
oraz![]() określonej wzorem
określonej wzorem
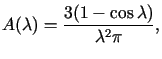
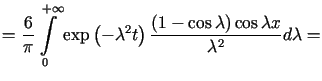 |
||
![$\displaystyle =\frac{3}{2\sqrt{\pi t}}\int\limits_{-1}^{+1}\left( 1-\left\vert r\right\vert \right) \exp\left[ -\frac{\left( r-x\right) ^{2}}{4t}\right] dr.$](img638.gif) |
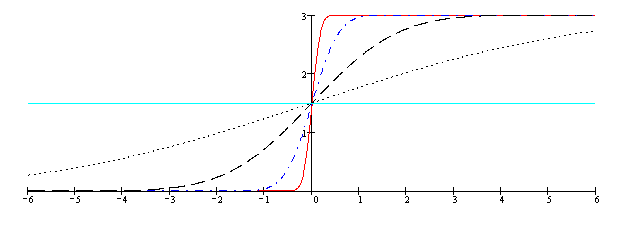
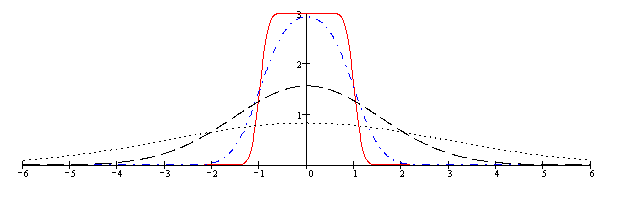
Kolejny rysunek przedstawia wykresy temperatury w różnych chwilach czasu. Poszczególne rodzaje linii odpowiadają czasom:
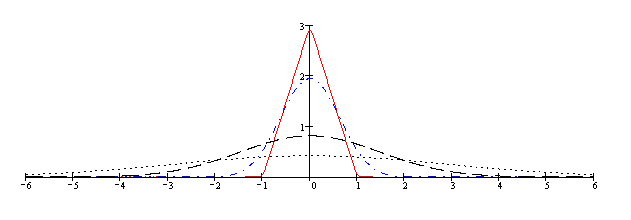
P r z y k ł a d 3
Rozwiązać powyższe zagadnienie początkowe dla ![]() oraz
oraz![]() określonej wzorem
określonej wzorem
Korzystając z faktu, że 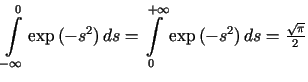 ,
otrzymujemy
,
otrzymujemy
![$\displaystyle =\frac{T_{2}}{2a\sqrt{\pi t}}<tex2html_comment_mark>654 {\display......^{+\infty}} \exp\left[ -\frac{\left( \tau-x\right) ^{2}}{4a^{2}t}\right] d\tau=$](img643.gif) |
||
![$\displaystyle =\left\vert \begin{array}[c]{cc}<tex2html_comment_mark>662 \frac{......style\int\limits_{-\frac{x}{2\sqrt{t}}}^{+\infty}} \exp\left( -s^{2}\right) ds=$](img644.gif) |
||
![$\displaystyle =\frac{T_{2}}{\sqrt{\pi}}\left[ \frac{\sqrt{\pi}}{2}-<tex2html_co......yle\int\limits_{-\frac{x}{2\sqrt{t}}}^{0}} \exp\left( -s^{2}\right) ds\right] =$](img645.gif) |
||
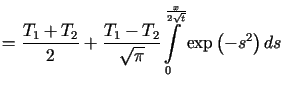 . . |
Rozważmy teraz przypadek szczególny ![]() ,
, ![]() .
.
Oto wykresy temperatury. Poszczególne linie odpowiadają różnym wartościom t.