



Next:ZadaniaUp:Równanie
przewodnictwa cieplnego (I)Previous:Zagadnienie
Cauchy'ego dla prętaSpis
rzeczy
Rozkład temperatury w pręcie
półograniczonym
Rozkład temperatury w jednowymiarowym półograniczonym pręcie, w którym
nie występują wewnętrzne źródła ciepła, opisuje funkcja 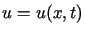 ,
spełniająca jednorodne równanie przewodnictwa cieplnego (4.1).
,
spełniająca jednorodne równanie przewodnictwa cieplnego (4.1).
Zakładamy, że dany jest początkowy rozkład temperatury
gdzie 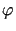 jest pewną daną funkcją ograniczoną, oraz stan temperatury na końcu pręta
w dowolnej chwili czasu
jest pewną daną funkcją ograniczoną, oraz stan temperatury na końcu pręta
w dowolnej chwili czasu 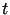
Rozwiązanie 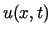 zagadnienia (4.1), (4.14),
(4.15) przedstawiamy w postaci
zagadnienia (4.1), (4.14),
(4.15) przedstawiamy w postaci
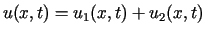 ,
, gdzie
gdzie 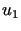 i
i 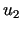 są rozwiązaniami rozważanego jednorodnego równania przewodnictwa spełniającymi
warunki
są rozwiązaniami rozważanego jednorodnego równania przewodnictwa spełniającymi
warunki
Korzystając z własności rozwiązania podstawowego równania przewodnictwa,
analogicznie jak w punkcie poprzednim, można wyprowadzić wzory
P r z y k ł a d
Rozwiązać powyższe zagadnienie dla ,
, 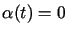 ,
,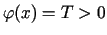 (chłodzenie pręta o ustalonej jednorodnej temperaturze początkowej).
(chłodzenie pręta o ustalonej jednorodnej temperaturze początkowej).
Z przedstawionych warunków oraz ze wzoru (4.17)
wynika, że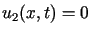 ,
zaś
,
zaś
![$\displaystyle u(x,t)=u_{1}(x,t)=\frac{T}{2\sqrt{\pi t}}\int\limits_{0}^{+\infty......u\right) ^{2}}{4t}\right] \right\} d\tau=T\Phi\left(\frac{x}{2\sqrt{t}}\right)$](img666.gif) ,
, gdzie
gdzie
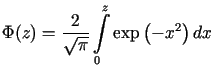 .
. Poniższy rysunek przedstawia wykresy temperatury w różnych chwilach czasu
(t=0,001, t=0,1, t=1, t=5, t=20) i przedziałach zmienności
Poniższy rysunek przedstawia wykresy temperatury w różnych chwilach czasu
(t=0,001, t=0,1, t=1, t=5, t=20) i przedziałach zmienności 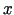 dla
dla 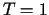 .
.
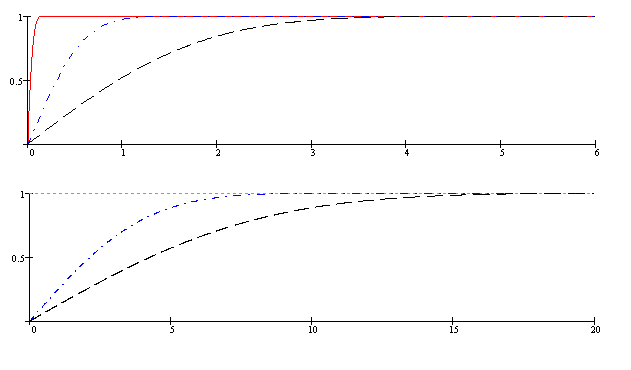 Wraz z upływem czasu następuje obniżenie temperatury we wszystkich punktach
pręta.
Wraz z upływem czasu następuje obniżenie temperatury we wszystkich punktach
pręta.




Next:ZadaniaUp:Równanie
przewodnictwa cieplnego (I)Previous:Zagadnienie
Cauchy'ego dla prętaSpis
rzeczy
Administrator 2003-02-05
![]() jest pewną daną funkcją ograniczoną, oraz stan temperatury na końcu pręta
w dowolnej chwili czasu
jest pewną daną funkcją ograniczoną, oraz stan temperatury na końcu pręta
w dowolnej chwili czasu ![]()
![]() zagadnienia (4.1), (4.14),
(4.15) przedstawiamy w postaci
zagadnienia (4.1), (4.14),
(4.15) przedstawiamy w postaci
![$\displaystyle =\frac{1}{2a\sqrt{\pi t}}\int\limits_{0}^{+\infty}\left\{ \exp\le...... -\frac{\left( x+\tau\right) ^{2}}{4a^{2}t}\right] \right\} \varphi (\tau)d\tau$](img660.gif) ,
,![$\displaystyle =\frac{x}{2a\sqrt{\pi}}\int\limits_{0}^{+\infty}\frac{\alpha (r)}{\sqrt{(t-r)^{3}}}\exp\left[ -\frac{x^{2}}{4a^{2}\left( t-r\right) }\right] dr$](img662.gif) dla
dla ![]() ,
, ![]() ,
,![]() (chłodzenie pręta o ustalonej jednorodnej temperaturze początkowej).
(chłodzenie pręta o ustalonej jednorodnej temperaturze początkowej).
![]() ,
zaś
,
zaś
![$\displaystyle u(x,t)=u_{1}(x,t)=\frac{T}{2\sqrt{\pi t}}\int\limits_{0}^{+\infty......u\right) ^{2}}{4t}\right] \right\} d\tau=T\Phi\left(\frac{x}{2\sqrt{t}}\right)$](img666.gif) ,
,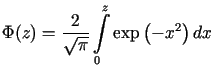 .
.