| (5.1) |
| (5.1) |
spełniającego warunki brzegowe
| (5.2) |
i warunek początkowy
| (5.3) |
Rozwiązanie zagadnienia (5.1)-(5.3) można znaleźć metodą Fouriera, podobnie jak w przypadku struny skończonej.
Podstawienie
sprowadza problem do przypadku jednorodnych warunków brzegowych, tak
więc wystarczy umieć rozwiązać zadanie dla ![]() ,
, ![]() .
.
Przedstawiamy szukaną funkcję ![]() w postaci
w postaci
oraz
Przedstawiając ![]() i rozdzielając zmienne, po przeprowadzeniu dyskusji wartości własnych odpowiedniego
zagadnienia Sturma-Liouville'a, otrzymujemy wzór na postać funkcji
i rozdzielając zmienne, po przeprowadzeniu dyskusji wartości własnych odpowiedniego
zagadnienia Sturma-Liouville'a, otrzymujemy wzór na postać funkcji ![]()
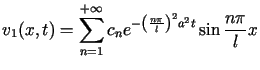 ,
gdzie ,
gdzie |
(5.4) | |
![$\displaystyle =\frac{2}{l}\int\limits_{0}^{l}\left[ \varphi(s)-w(s,0)\right] \sin\frac{n\pi}{l}sds$](img702.gif) , , |
(5.5) |
Analogicznie, jak w przypadku struny, otrzymujemy przedstawienie funkcji![]() w postaci szeregu
w postaci szeregu
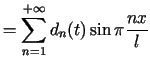 ,
gdzie ,
gdzie |
(5.6) | |
![$\displaystyle =\frac{2}{l}\int\limits_{0}^{t}e^{-\left( \frac{n\pi}{l}\right) ^......l}\left[ f(s,\tau)-w_{\tau }(s,\tau)\right] \sin\frac{n\pi}{l}sds\right\} d\tau$](img706.gif) , , |
(5.7) |
Założenia, które należy przyjąć o funkcjach danych są analogiczne do
założeń dla odpowiedniego zagadnienia dla struny skończonej.
P r z y k ł a d 1
Rozwiązać powyższe zagadnienie początkowe dla ![]() ,
, ![]() ,
,![]() ,
, ![]() ,
, ![]() ,
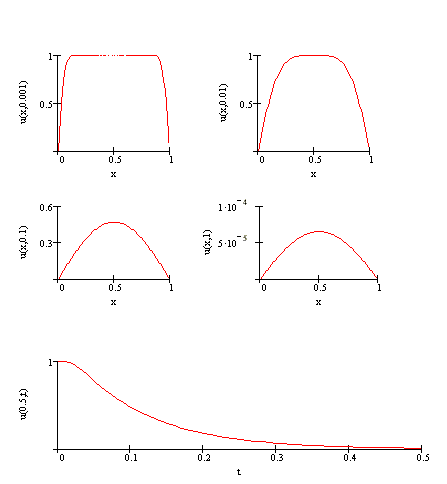
, ![]() (chłodzenie pręta o ustalonej jednorodnej temperaturze początkowej).
(chłodzenie pręta o ustalonej jednorodnej temperaturze początkowej).
Z przedstawionych warunków wynika, że
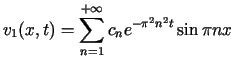 ,
,![$\displaystyle c_{n}=\frac{2}{\pi n}\left[ 1-(-1)^{n}\right]$](img715.gif) dla
dla 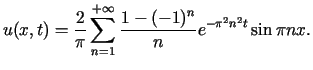
P r z y k ł a d 2
Rozwiązać powyższe zagadnienie początkowe dla ![]()
![]()
![]()
![]()
![]()
![]() .
.
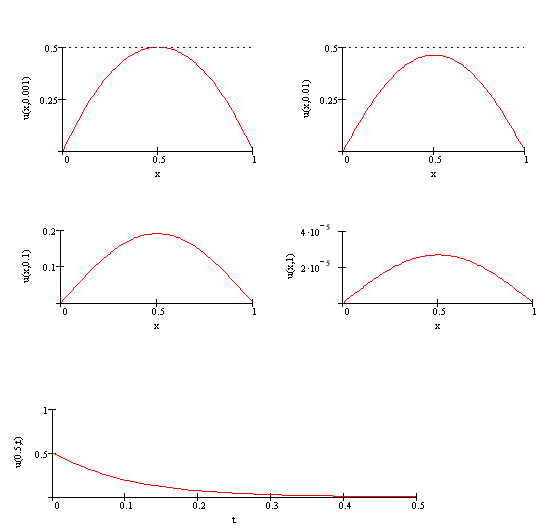
Z warunków zadania wynika, że
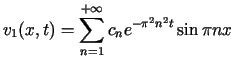 ,
,![$\displaystyle c_{n}=\frac{8}{(\pi n)^{3}}\left[ 1-(-1)^{n}\right]$](img723.gif) dla
dla 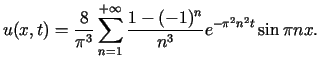
P r z y k ł a d 3
Rozwiązać powyższe zagadnienie początkowe dla ![]()
![]()
![]()
![]()
![]()
![]() (podgrzewanie pręta od prawego końca).
(podgrzewanie pręta od prawego końca).
Z warunków zadania wynika, że
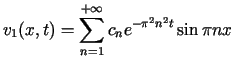 ,
,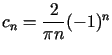 dla
dla 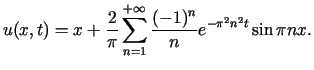
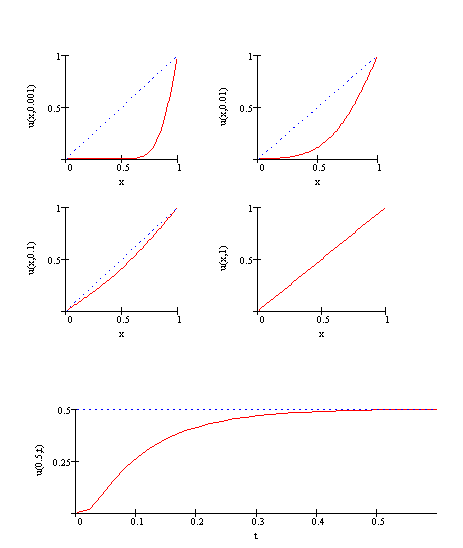
| (5.8) |
Zachodzi następujące twierdzenie zwane zasadą maksimum dla równania
przewodnictwa cieplnego.
T w i e r d z e n i e (zasada maksimum)
Jeśli funkcja ![]() określona i ciągła w obszarze
określona i ciągła w obszarze ![]() ,
, ![]() spełnia jednorodne równanie przewodnictwa (5.8)
w punktach obszaru
spełnia jednorodne równanie przewodnictwa (5.8)
w punktach obszaru ![]() ,
, ![]() ,
to osiąga ona swoje kresy w chwili początkowej
,
to osiąga ona swoje kresy w chwili początkowej ![]() lub dla
lub dla ![]() lub dla
lub dla![]() .
.
Sens fizyczny tego twierdzenia jest następujący: jeśli temperatura na
brzegu pręta nie przekracza pewnej wartości ![]() i początkowa temperatutra także nie przekracza
i początkowa temperatutra także nie przekracza ![]() ,
to wewnątrz pręta, przy braku źródeł ciepła, nie może pojawić się temperatura
wyższa niż
,
to wewnątrz pręta, przy braku źródeł ciepła, nie może pojawić się temperatura
wyższa niż ![]() .
.
W n i o s e k
Jeśli ![]() i
i ![]() są dwoma rozwiązaniami równania (5.1) i spełnione
są warunki
są dwoma rozwiązaniami równania (5.1) i spełnione
są warunki
to dla dowolnych ![]() ,
, ![]() zachodzi nierówność
zachodzi nierówność
Rozważając funkcję ![]() stwierdzamy, że spełnia ona równanie (5.8),
a ponadto warunki
stwierdzamy, że spełnia ona równanie (5.8),
a ponadto warunki
T w i e r d z e n i e
Jeśli ![]() i
i ![]() są rozwiązaniami równania (5.1) takimi, że
warunki brzegowe i początkowy spełniają nierówność
są rozwiązaniami równania (5.1) takimi, że
warunki brzegowe i początkowy spełniają nierówność
| (5.9) |
to
D o w ó d
Warunek (5.9) można zapisać w postaci
Podstawiając z kolei ![]() i
i ![]() otrzymujemy nierówność
otrzymujemy nierówność ![]() co kończy dowód twierdzenia.
co kończy dowód twierdzenia.