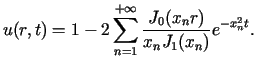Next:ZadaniaUp:Równanie
przewodnictwa cieplnego (II)Previous:Metoda
Fouriera dla prętaSpis
rzeczy
Subsections
Przykłady radialnego rozkładu
ciepła w walcu
Zagadnienie ostygania walca
Rozważamy walec o promieniu 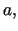 którego osią jest
którego osią jest 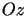 .
Niech
.
Niech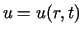 oznacza temperaturę punktu walca oddalonego od jego osi o
oznacza temperaturę punktu walca oddalonego od jego osi o 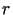 ,
w chwili
,
w chwili 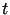 .
Funkcja ta spełnia równanie przewodnictwa (we współrzędnych biegunowych)
postaci
.
Funkcja ta spełnia równanie przewodnictwa (we współrzędnych biegunowych)
postaci
Załóżmy, że powierzchnia boczna walca utrzymywana jest w temperaturze
0, a więc spełniony jest jednorodny warunek brzegowy
Zakładamy również spełnianie osiowosymetrycznego warunku początkowego
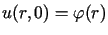 dla
dla 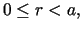 |
(5.12) |
gdzie 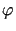 jest funkcją daną, która może być przedstawiona w postaci szeregu Fouriera
- Bessela.
jest funkcją daną, która może być przedstawiona w postaci szeregu Fouriera
- Bessela.
Stosując metodę Fouriera (rozdzielenia zmiennych) dla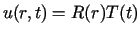 otrzymujemy dwa równania
otrzymujemy dwa równania
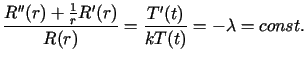 Z warunku brzegowego wynika, że stały parametr
Z warunku brzegowego wynika, że stały parametr 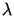 może przyjmować wartości
może przyjmować wartości
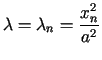 ,
dla
,
dla 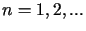 ,
, gdzie
gdzie 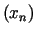 jest ciągiem dodatnich zer funkcji Bessela
jest ciągiem dodatnich zer funkcji Bessela 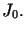 W takim razie funkcja
W takim razie funkcja
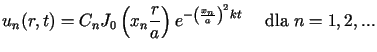 i dowolnej stałej
i dowolnej stałej 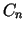 jest rozwiązaniem rozważanego równania spełniającym jednocześnie jednorodny
warunek brzegowy
jest rozwiązaniem rozważanego równania spełniającym jednocześnie jednorodny
warunek brzegowy 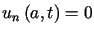 .
.
Pełnym rozwiązaniem zagadnienia (5.10)-(5.12),
speł niającym także warunek początkowy, jest funkcja 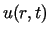 określona jako suma szeregu
określona jako suma szeregu
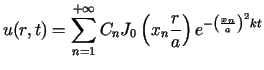 |
(5.13) |
gdzie stałe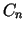 wyznaczone są za pomocą wzorów
wyznaczone są za pomocą wzorów
P r z y k ł a d
Rozwiązać zagadnienie ostygania walca dla 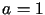 ,
, 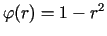 .
.
Zgodnie za wzorem (5.14)
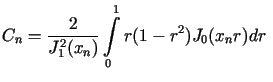 dla
dla 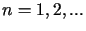 Korzystając z własności funkcji Bessela oraz stosując wzór na całkowanie
przez części otrzymujemy ostatecznie
Korzystając z własności funkcji Bessela oraz stosując wzór na całkowanie
przez części otrzymujemy ostatecznie
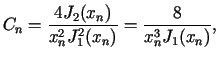 a zatem zgodnie ze wzorem (5.13) rozwiązanie
a zatem zgodnie ze wzorem (5.13) rozwiązanie 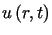 zagadnienia wyraża się wzorem
zagadnienia wyraża się wzorem
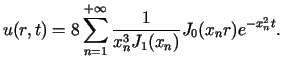 Poniższy rysunek przedstawia wykresy temperatury
Poniższy rysunek przedstawia wykresy temperatury 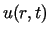 dla
dla 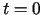 ,
,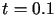 ,
,  .
.
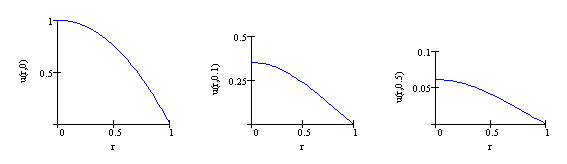 W miarę upływu czasu następuje obniżenie temperatury we wszystkich punktach
walca.
W miarę upływu czasu następuje obniżenie temperatury we wszystkich punktach
walca.
Zagadnienie nagrzewania powierzchni
bocznej walca
Rozważamy walec o promieniu 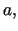 którego osią jest
którego osią jest 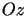 .
Niech
.
Niech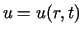 oznacza temperaturę punktu walca oddalonego od jego osi o
oznacza temperaturę punktu walca oddalonego od jego osi o 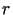 ,
w chwili
,
w chwili 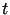 .
Funkcja ta spełnia równanie przewodnictwa postaci (5.10).
.
Funkcja ta spełnia równanie przewodnictwa postaci (5.10).
Załóżmy, że powierzchnia boczna walca utrzymywana jest w temperaturze 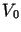 ,
a więc spełniony jest warunek brzegowy
,
a więc spełniony jest warunek brzegowy
Zakładamy również spełnianie jednorodnego warunku początkowego
Niech 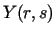 będzie transformatą Laplace'a funkcji
będzie transformatą Laplace'a funkcji 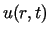 względem zmiennej
względem zmiennej 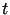 .
Wtedy
.
Wtedy 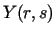 spełnia równanie
spełnia równanie
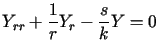 . . |
(5.17) |
Warunek brzegowy (5.15) implikuje równość
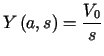 . . |
(5.18) |
Rozwiązaniem równania (5.17) spełniającym
jednocześnie warunek brzegowy (5.18) jest
funkcja
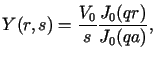 gdzie
gdzie 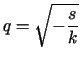 .
. Odwracając transformatę Laplace'a np. za pomocą twierdzenia o residuach,
otrzymujemy ostatecznie wzór na rozwiązanie zagadnienia
Odwracając transformatę Laplace'a np. za pomocą twierdzenia o residuach,
otrzymujemy ostatecznie wzór na rozwiązanie zagadnienia
![$\displaystyle u(r,t)=V_{0}\left[ 1-2\sum\limits_{n=1}^{+\infty}\frac{J_{0}\left......n})}e^{-\left( \frac{x_{n}}<tex2html_comment_mark>764 {a}\right) ^{2}kt}\right]$](img809.gif) , , |
(5.19) |
gdzie 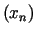 jest ciągiem dodatnich zer funkcji Bessela
jest ciągiem dodatnich zer funkcji Bessela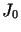 .
.
P r z y k ł a d
Rozwiązać powyższe zagadnienie dla 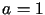 ,
, 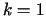 ,
, 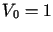 .
.
Na podstawie wzoru (5.19) możemy napisać,
że
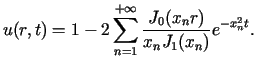 Linie w kolorze niebieskim są wykresami funkcji
Linie w kolorze niebieskim są wykresami funkcji 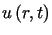 dla
dla 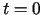 ,
, 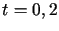 ,
, 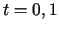 ,
zaś linia czerwona jest wykresem temperatury jako funkcji czasu w punkcie
położonym na osi walca (
,
zaś linia czerwona jest wykresem temperatury jako funkcji czasu w punkcie
położonym na osi walca (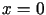 ).
).
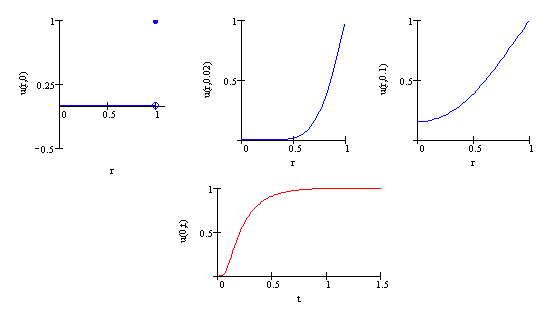
W miarę upływu czasu następuje wzrost temperatury do wartości 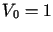 we wszystkich punktach walca.
we wszystkich punktach walca.




Next:ZadaniaUp:Równanie
przewodnictwa cieplnego (II)Previous:Metoda
Fouriera dla prętaSpis
rzeczy
Administrator 2003-02-08
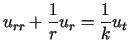 dla
dla 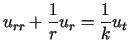 dla
dla ![]() jest funkcją daną, która może być przedstawiona w postaci szeregu Fouriera
- Bessela.
jest funkcją daną, która może być przedstawiona w postaci szeregu Fouriera
- Bessela.
![]() otrzymujemy dwa równania
otrzymujemy dwa równania
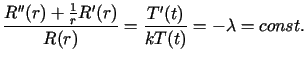
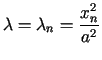 ,
dla
,
dla 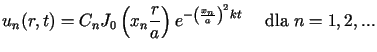
![]() określona jako suma szeregu
określona jako suma szeregu
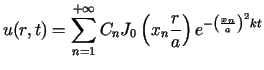
![]() wyznaczone są za pomocą wzorów
wyznaczone są za pomocą wzorów
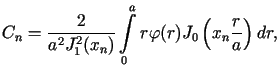 dla
dla ![]() ,
, ![]() .
.
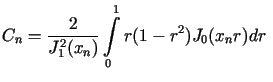 dla
dla 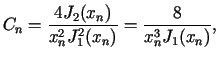
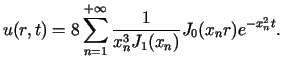

![]() ,
a więc spełniony jest warunek brzegowy
,
a więc spełniony jest warunek brzegowy
![]() będzie transformatą Laplace'a funkcji
będzie transformatą Laplace'a funkcji ![]() względem zmiennej
względem zmiennej ![]() .
Wtedy
.
Wtedy ![]() spełnia równanie
spełnia równanie
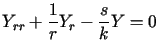 .
.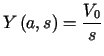 .
.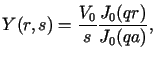 gdzie
gdzie 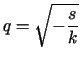 .
.![$\displaystyle u(r,t)=V_{0}\left[ 1-2\sum\limits_{n=1}^{+\infty}\frac{J_{0}\left......n})}e^{-\left( \frac{x_{n}}<tex2html_comment_mark>764 {a}\right) ^{2}kt}\right]$](img809.gif) ,
,![]() jest ciągiem dodatnich zer funkcji Bessela
jest ciągiem dodatnich zer funkcji Bessela![]() .
.
![]() ,
, ![]() ,
, ![]() .
.