



Next:Klasyfikacja
prawie-liniowych r.r.cz. IIUp:Pojęcia
podstawowePrevious:Pojęcia
podstawoweSpis
rzeczy
Subsections
Przegląd wybranych równań i modeli
fizycznych
Równaniem różniczkowym cząstkowym rzędu drugiego o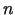 zmiennych
niezależnych nazywamy równanie postaci
zmiennych
niezależnych nazywamy równanie postaci
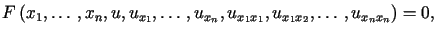  |
(1.1) |
gdzie 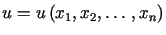 .
.
Równania opisujące ruch falowy
Zjawiska drgań poprzecznych struny jednowymiarowej, drgań podłużnych prętów,
drgań elektrycznych w przewodach opisane są równaniem
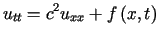 , , |
(1.2) |
które jest szczególnym przypadkiem równania (1.1)
dla 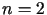 ,
,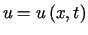 .
.
Drgania poprzeczne membrany opisuje równanie
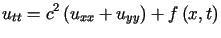 ,
, które spełnia funkcja
które spełnia funkcja 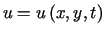 - wychylenie z położenia równowagi (
- wychylenie z położenia równowagi (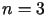 ),
zaś równanie fali akustycznej jest postaci
),
zaś równanie fali akustycznej jest postaci
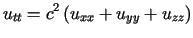 ,
, gdzie
gdzie 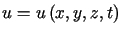 oznacza tzw. potencjał prędkości (
oznacza tzw. potencjał prędkości (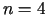 ).
).
Wszystkie powyżej rozważane równania można jednolicie zapisać używając
tzw. operatora Laplace'a 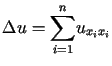 (względem zmiennych przestrzennych) w postaci
(względem zmiennych przestrzennych) w postaci
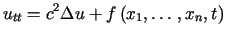 .
. |
(1.3) |
Równania przewodnictwa cieplnego
i dyfuzji
Zjawisko przewodnictwa cieplnego w pręcie jednowymiarowym opisane jest
równaniem
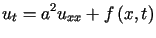 , , |
(1.4) |
gdzie funkcja 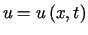 oznacza temperaturę w punkcie
oznacza temperaturę w punkcie 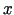 ,
w chwili
,
w chwili 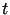 ,
zaś
,
zaś 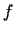 opisuje działające źródła ciepła. Również zjawisko dyfuzji gazu lub cieczy
opisane jest równaniem (1.4), gdzie
opisuje działające źródła ciepła. Również zjawisko dyfuzji gazu lub cieczy
opisane jest równaniem (1.4), gdzie 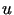 oznacza stężenie obserwowanego składnika.
oznacza stężenie obserwowanego składnika.
Rozchodzenie się ciepła w przestrzeni można opisać równaniem
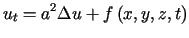 , , |
(1.5) |
gdzie 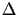 jest operatorem Laplace'a
jest operatorem Laplace'a 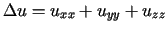 .
.
Zagadnienia prowadzące do równania
Laplace'a i równania Poissona
Stacjonarne (niezmienne w czasie) pole temperatur 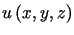 spełnia równanie Laplace'a
spełnia równanie Laplace'a
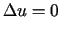 , , |
(1.6) |
co wynika bezpośrednio z równania (1.5),
w którym 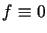 .
Powyższe równanie spełnione jest także przez potencjał pola grawitacyjnego
i elektrostatycznego w próżni.
.
Powyższe równanie spełnione jest także przez potencjał pola grawitacyjnego
i elektrostatycznego w próżni.
Gdy gęstość masy (ładunków elektrostatycznych) wynosi 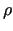 ,
to wówczas odpowiednie potencjały spełniają tzw. równanie Poissona
,
to wówczas odpowiednie potencjały spełniają tzw. równanie Poissona
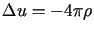 .
. Szeroka klasa zagadnień związanych z drganiami ustalonymi prowadzi do tzw.
równania
Helmholtza
Szeroka klasa zagadnień związanych z drganiami ustalonymi prowadzi do tzw.
równania
Helmholtza
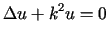 .
.




Next:Klasyfikacja
prawie-liniowych r.r.cz. IIUp:Pojęcia
podstawowePrevious:Pojęcia
podstawoweSpis
rzeczy
Administrator 2003-02-13
![]() .
.
![]() ,
,![]() .
.
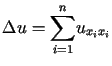 (względem zmiennych przestrzennych) w postaci
(względem zmiennych przestrzennych) w postaci
![]() oznacza temperaturę w punkcie
oznacza temperaturę w punkcie ![]() ,
w chwili
,
w chwili ![]() ,
zaś
,
zaś ![]() opisuje działające źródła ciepła. Również zjawisko dyfuzji gazu lub cieczy
opisane jest równaniem (1.4), gdzie
opisuje działające źródła ciepła. Również zjawisko dyfuzji gazu lub cieczy
opisane jest równaniem (1.4), gdzie ![]() oznacza stężenie obserwowanego składnika.
oznacza stężenie obserwowanego składnika.
![]() jest operatorem Laplace'a
jest operatorem Laplace'a ![]() .
.
![]() .
Powyższe równanie spełnione jest także przez potencjał pola grawitacyjnego
i elektrostatycznego w próżni.
.
Powyższe równanie spełnione jest także przez potencjał pola grawitacyjnego
i elektrostatycznego w próżni.
![]() ,
to wówczas odpowiednie potencjały spełniają tzw. równanie Poissona
,
to wówczas odpowiednie potencjały spełniają tzw. równanie Poissona