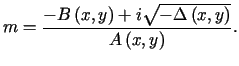| (1.7) |
| (1.7) |
W szczególności, równania (1.2), (1.4)
i (1.6) dla![]() są tej postaci.
są tej postaci.
Wprowadzamy wyróżnik ![]() i w zależności od jego znaku mówimy, że równanie (1.7)
jest w punkcie
i w zależności od jego znaku mówimy, że równanie (1.7)
jest w punkcie ![]() typu:
typu:
Załóżmy, że dane jest przekształcenie ![]() ,
, ![]() określone dla
określone dla ![]() .
Zakładamy, że jest ono nieosobliwe, tzn. jego jakobian spełnia warunek
.
Zakładamy, że jest ono nieosobliwe, tzn. jego jakobian spełnia warunek
| (1.8) |
T w i e r d z e n i e
Typ równania (1.7) jest niezmienniczy ze
względu na nieosobliwą zamianę zmiennych (1.8).
Dowód twierdzenia wynika z faktu, że po dokonaniu zamiany zmiennych
w równaniu jego ,,nowy''wyróżnik ![]() spełnia zależność
spełnia zależność
![$\displaystyle \Delta^{\prime}=\left[ \frac{\partial\left( \xi,\eta\right) }%%{\partial\left( x,y\right) }\right] ^{2}\Delta$](img45.gif) ,
, Prawdziwe są następujące twierdzenia dotyczące poszczególnych typów
równań prawie-liniowych postaci (1.7).
T w i e r d z e n i e
Jeśli równanie (1.7) jest hiperboliczne w
obszarze ![]() i
i ![]() lub
lub ![]() ,
to istnieje nieosobliwe przekształcenie
,
to istnieje nieosobliwe przekształcenie ![]() ,
, ![]() ,
, ![]() takie, że równanie (1.7) we współrzędnych
takie, że równanie (1.7) we współrzędnych ![]() ,
, ![]() przybiera postać
przybiera postać
| (1.9) |
zwaną pierwszą postacią kanoniczną równania (1.7)
w przypadku hiperbolicznym. Funkcje ![]() i
i![]() są całkami pierwszymi układu równań różniczkowych zwyczajnych
są całkami pierwszymi układu równań różniczkowych zwyczajnych
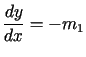 ,
, 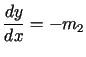 ,
,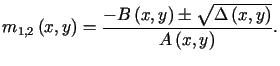
T w i e r d z e n i e
Jeżeli równanie (1.7) jest paraboliczne w
obszarze ![]() i
i ![]() ,
to istnieje nieosobliwe przekształcenie
,
to istnieje nieosobliwe przekształcenie ![]() ,
,![]() ,
, ![]() takie, że równanie (1.7) we współrzędnych
takie, że równanie (1.7) we współrzędnych ![]() ,
, ![]() przybiera postać
przybiera postać
| (1.10) |
zwaną postacią kanoniczną równania typu parabolicznego o
dwóch zmiennych niezależnych. Funkcja ![]() jest całką pierwszą równania różniczkowego zwyczajnego
jest całką pierwszą równania różniczkowego zwyczajnego
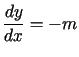 ,
gdzie
,
gdzie 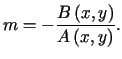
T w i e r d z e n i e
Jeżeli równanie (1.7) jest eliptyczne w obszarze ![]() i
i ![]() ,
, ![]() ,
,![]() są analityczne, to istnieje nieosobliwe przekształcenie
są analityczne, to istnieje nieosobliwe przekształcenie ![]() ,
, ![]() ,
, ![]() takie, że równanie (1.7) we współrzędnych
takie, że równanie (1.7) we współrzędnych ![]() ,
, ![]() przybiera postać
przybiera postać
| (1.11) |
zwaną postacią kanoniczną równania typu eliptycznego o dwóch
zmiennych niezależnych. Funkcje ![]() i
i![]() określone są zależnościami
określone są zależnościami![]() ,
, ![]() ,
gdzie
,
gdzie ![]() jest całką pierwszą, równania różniczkowego zwyczajnego
jest całką pierwszą, równania różniczkowego zwyczajnego
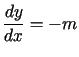 ,
gdzie
,
gdzie