D e f i n i c j a
D (zbiór funkcji próbnych) ![]() lub
lub ![]() .
.
Oznacza to, że ![]() oraz
oraz ![]() (nośnik funkcji) jest zwarty (
(nośnik funkcji) jest zwarty (![]() może być funkcją o wartościach rzeczywistych lub zespolonych).
może być funkcją o wartościach rzeczywistych lub zespolonych).
W przestrzeni funkcji próbnych definiujemy zbieżność ciągu funkcyjnego
w sposób następujący.
D e f i n i c j a
![]() w
w ![]()
![]() oraz nośniki
oraz nośniki ![]() są wspólnie ograniczone.
są wspólnie ograniczone.
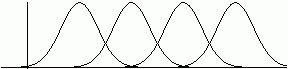
T w i e r d z e n i e
Każda funkcja ciągła ![]() o nośniku ograniczonym może być jednostajnie przybliżona przez funkcje
z przestrzeni D.
o nośniku ograniczonym może być jednostajnie przybliżona przez funkcje
z przestrzeni D.
Dla dowodu twierdzenia należy rozważyć funkcję
![\begin{displaymath}\xi\left( t\right) =\left\{\begin{array}[c]{rl}%%0 & \text......t{dla }\left\vert t\right\vert <1\text{,}%%\end{array}\right.\end{displaymath}](img1055.gif)
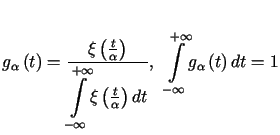
Niech
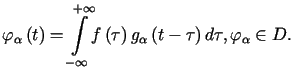
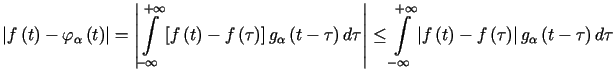 .
.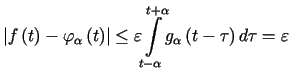
D e f i n i c j a
Przestrzenią dystrybucji ![]() nazywamy przestrzeń funkcjonałów liniowych i ciągłych na D (względem zbieżności
określonej w poprzedniej definicji).
nazywamy przestrzeń funkcjonałów liniowych i ciągłych na D (względem zbieżności
określonej w poprzedniej definicji).
W przestrzeni ![]() określamy zbieżność jak następuje. Niech
określamy zbieżność jak następuje. Niech ![]() ,
, ![]() (oznaczamy równoważnie
(oznaczamy równoważnie![]() ).
).
D e f i n i c j a
![]() w
w ![]()
![]()
T w i e r d z e n i e
Przestrzeń![]() jest domknięta ze względu na zbieżność (tzn. granica ciągu funkcjonałów
liniowych i ciągłych jest funkcjonałem liniowym i ciągłym).
jest domknięta ze względu na zbieżność (tzn. granica ciągu funkcjonałów
liniowych i ciągłych jest funkcjonałem liniowym i ciągłym).
Spośród wszystkich dystrybucji szczególnie wyróżniamy tzw. dystrybucje
regularne. Są to dystrybucje wyznaczone przez funkcje lokalnie całkowalne.
Niech ![]() będzie funkcją lokalnie całkowalną na
będzie funkcją lokalnie całkowalną na![]() ,
a więc funkcją, dla której istnieje całka oznaczona po dowolnym przedziale
skończonym z funkcji
,
a więc funkcją, dla której istnieje całka oznaczona po dowolnym przedziale
skończonym z funkcji ![]() .
.
D e f i n i c j a
Dystrybucją regularną wyznaczoną przez lokalnie całkowalną funkcję ![]() nazywamy dystrybucję określoną wzorem
nazywamy dystrybucję określoną wzorem
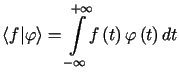
Poprawność tej definicji (ciągłość funkcjonału) wynika z oszacowania
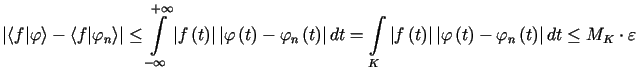
Wiele własności dystrybucji i pojęć z nimi związanych wprowadza się
w ten sposób, by były one uogólnieniem własności dystrybucji regularnych.
Dotyczy to przede wszystkim różniczkowania dystrybucji, pojęcia
równości
dystrybucji na zbiorze otwartym (mimo, że dystrybucja nie jest funkcją
mającą określoną wartość w każdym punkcie) oraz pojęcia nośnika dystrybucji.
Rozważmy na początek funkcję lokalnie całkowalną ![]() ,
której pochodna
,
której pochodna ![]() jest także funkcją lokalnie całkowalną. Niech
jest także funkcją lokalnie całkowalną. Niech ![]() będzie taka, że
będzie taka, że![]() -
zwarty. Wówczas ze wzoru na całkowanie przez części otrzymujemy
-
zwarty. Wówczas ze wzoru na całkowanie przez części otrzymujemy
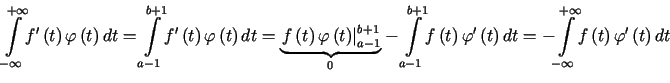
D e f i n i c j a
Pochodną dystrybucji![]() nazywamy dystrybucję
nazywamy dystrybucję![]() określoną wzorem
określoną wzorem
| (8.1) |
dla ![]() (w ten sposób każda dystrybucja, a więc i każda funkcja lokalnie całkowalna,
ma pochodną). Pochodną tą nazywamy pochodną w sensie dystrybucyjnym.
(w ten sposób każda dystrybucja, a więc i każda funkcja lokalnie całkowalna,
ma pochodną). Pochodną tą nazywamy pochodną w sensie dystrybucyjnym.
W przypadku wielowymiarowym powyższą definicję modyfikujemy do wzoru
| (8.2) |
gdzie ![]() jest
wielowskaźnikiem
jest
wielowskaźnikiem ![]() ,
, ![]() ,
zaś
,
zaś
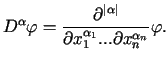 |
(8.3) |
D e f i n i c j a
Dystrybucje ![]() ,
,![]() są równe na zbiorze otwartym
są równe na zbiorze otwartym![]() wtedy i tylko wtedy gdy spełniony jest warunek
wtedy i tylko wtedy gdy spełniony jest warunek
D e f i n i c j a
Nośnikiem dystrybucji![]() nazywamy najmniejszy zbiór domknięty
nazywamy najmniejszy zbiór domknięty ![]() taki, że
taki, że ![]() na
na ![]() w sensie poprzedniej definicji.
w sensie poprzedniej definicji.
Spośród wszystkich dystrybucji wyrózniamy tzw. dystrybucje skończonego rzędu będące pochodnymi dystrybucyjnymi funkcji ciągłych.
D e f i n i c j a
Dystrybucję ![]() nazywamy dystrybucją skończonego rzędu wtedy i tylko wtedy gdy istnieje
funkcja
nazywamy dystrybucją skończonego rzędu wtedy i tylko wtedy gdy istnieje
funkcja ![]() ciągła na
ciągła na ![]() oraz liczba naturalna
oraz liczba naturalna ![]() taka, że
taka, że ![]() .
Najmniejszą liczbę
.
Najmniejszą liczbę ![]() o tej własności nazywamy rzędem dystrybucji T.
o tej własności nazywamy rzędem dystrybucji T.
T w i e r d z e n i e
Każda dystrybucja ![]() jest lokalnie dystrybucją skończonego rzędu tzn., że dla ustalonego ograniczonego
lecz dowolnego przedziału
jest lokalnie dystrybucją skończonego rzędu tzn., że dla ustalonego ograniczonego
lecz dowolnego przedziału ![]() istnieje
istnieje ![]() ,
, ![]() taka, że
taka, że ![]()
![]() zachodzi
zachodzi
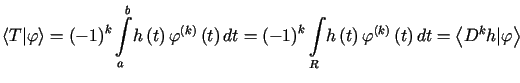 |
(8.4) |
(dla dystrybucji skończonego rzędu równość powyższa zachodzi dla wszystkich ![]() - bez żadnych dodatkowych ograniczeń co do nośnika
- bez żadnych dodatkowych ograniczeń co do nośnika ![]() ).
).
T w i e r d z e n i e
Niech ![]() będzie lokalnie całkowalna na
będzie lokalnie całkowalna na ![]() .
Niech
.
Niech 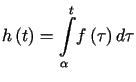 .
Wówczas
.
Wówczas ![]() (w sensie dystrybucyjnym).
(w sensie dystrybucyjnym).
W teorii całki Lebesgue'a dowodzi się, że ![]() jest różniczkowalna prawie wszędzie (tzn. ewentualnie poza zbiorem miary
zero) i prawie wszędzie
jest różniczkowalna prawie wszędzie (tzn. ewentualnie poza zbiorem miary
zero) i prawie wszędzie ![]() .
W takim razie mamy na mocy wzoru na całkowanie przez części
.
W takim razie mamy na mocy wzoru na całkowanie przez części
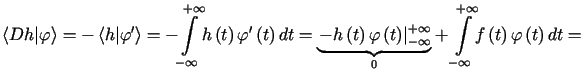 |
||
Ponieważ ![]() jest ciągła, więc
jest ciągła, więc ![]() jest skończonego rzędu (0 - gdy
jest skończonego rzędu (0 - gdy ![]() ciągła, 1 - w przeciwnym razie).
ciągła, 1 - w przeciwnym razie).
Niech
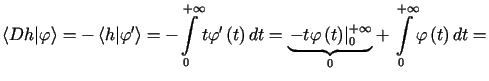 |
||
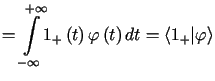 a więc
a więc |
P r z y k ł a d 2
Niech ![]() .
Obliczmy wartość
.
Obliczmy wartość ![]() .
.
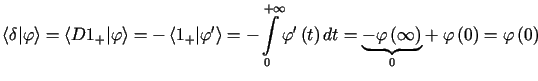
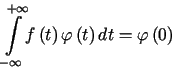 ,
jest ona jednakże dystrybucją skończonego rzędu, jej rząd równy jest 2.
,
jest ona jednakże dystrybucją skończonego rzędu, jej rząd równy jest 2.
P r z y k ł a d 3
Dystrybucje ![]() (pochodne delty Diraca) są także dystrybucjami skończonego (
(pochodne delty Diraca) są także dystrybucjami skończonego (![]() - go) rzędu. Korzystając z definicji obliczamy natychmiast, że
- go) rzędu. Korzystając z definicji obliczamy natychmiast, że