D e f i n i c j a
Dla dystrybucji ![]() definiujemy przekształcenie Laplace'a wzorem
definiujemy przekształcenie Laplace'a wzorem
T w i e r d z e n i e
Jeśli funkcja ![]() posiada
posiada ![]() transformatę w sensie klasycznym, to posiada również transformatę w sensie
dystrybucyjnym i transformaty te są równe.
transformatę w sensie klasycznym, to posiada również transformatę w sensie
dystrybucyjnym i transformaty te są równe.
Niech 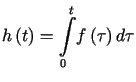 oraz niech
oraz niech ![]() w sensie klasycznym. Wówczas
w sensie klasycznym. Wówczas ![]() spełnia warunki 1 i 2 oraz
spełnia warunki 1 i 2 oraz ![]() .
Ponadto, zgodnie z tw. o transformacie całki w sensie klasycznym
.
Ponadto, zgodnie z tw. o transformacie całki w sensie klasycznym ![]() .
Zatem z poprzedniej definicji wynika, że wyznaczając tę transformatę w
sensie dystrybucyjnym dostajemy
.
Zatem z poprzedniej definicji wynika, że wyznaczając tę transformatę w
sensie dystrybucyjnym dostajemy
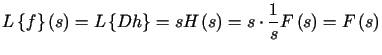
![]() .
Ponieważ
.
Ponieważ ![]() ,
gdzie
,
gdzie ![]() spełnia 1 i 2, więc
spełnia 1 i 2, więc
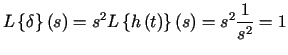
P r z y k ł a d 2
![]() .
Ponieważ
.
Ponieważ ![]() ,
więc
,
więc
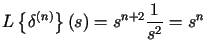 (wielomian).
(wielomian).
P r z y k ł a d 3
![]() ,
gdzie
,
gdzie ![]() .
Ponieważ
.
Ponieważ![]() ,
więc na mocy własności klasycznej transformaty (tw. o przesunięciu) otrzymujemy
,
więc na mocy własności klasycznej transformaty (tw. o przesunięciu) otrzymujemy
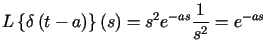 .
.Niech ![]() .
Wówczas operator przesunięcia
.
Wówczas operator przesunięcia ![]() określony na funkcjach próbnych równością
określony na funkcjach próbnych równością![]() definiujemy w przestrzeni dystrybucji jako
definiujemy w przestrzeni dystrybucji jako
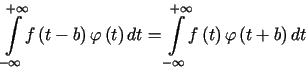 .
.Przykładowo, ![]() - por. przykład 3.
- por. przykład 3.
T w i e r d z e n i e (o przesunięciu)
Dla każdego ![]() prawdziwy jest wzór
prawdziwy jest wzór
Dla dowodu zauważmy, że
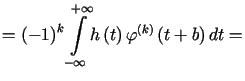 |
||
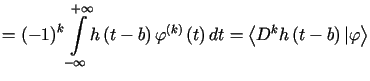 |
co oznacza, że ![]() Zatem
Zatem
Analogicznie do operatora przesunięcia wprowadzamy w przestrzeni dystrybucji
operację
mnożenia dystrybucji przez funkcję klasy![]() .
Ponieważ dla
.
Ponieważ dla ![]() - lokalnie całkowalnych,
- lokalnie całkowalnych,![]() ,
, ![]() zachodzi oczywisty wzór
zachodzi oczywisty wzór
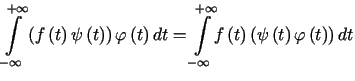 ,
,D e f i n i c j a (mnożenia dystrybucji przez funkcje klasy ![]() )
)
![]() .
.
T w i e r d z e n i e (przesunięcie w dziedzinie zespolonej)
Jeżeli ![]() ,
, ![]() ,
to zachodzi wzór
,
to zachodzi wzór
Dla dowodu skorzystamy ze wzoru Leibniza na pochodną iloczynu funkcji.
Niech ![]() .
Wówczas otrzymujemy
.
Wówczas otrzymujemy
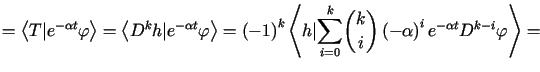 |
||
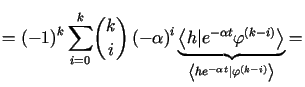 |
||
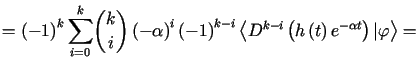 |
||
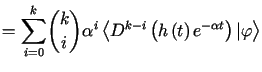 . . |
W takim razie 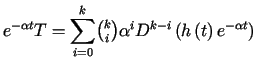 ,
a więc
,
a więc
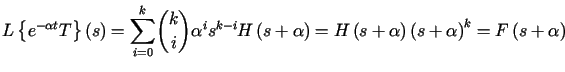
T w i e r d z e n i e (o transformacie pochodnej)
Jeśli ![]() ,
, ![]() ,
to prawdziwy jest wzór
,
to prawdziwy jest wzór
Niech ![]() ,
zatem
,
zatem ![]() .
Stąd
.
Stąd
U w a g a
Powyższy wzór różni się pozornie od sformułowania klasycznego. W sformułowamiu klasycznym prawdziwy jest wzór
| (8.5) |
Występująca między obydwoma przypadkami różnica jest jednak tylko pozorna.
Jeżeli oznaczymy przez ![]() dystrybucję generowaną przez funkcję
dystrybucję generowaną przez funkcję ![]() (równą 0 dla
(równą 0 dla![]() ),
to łatwo pokazać przez indukcję względem n, że pochodna w sensie dystrybucyjnym
),
to łatwo pokazać przez indukcję względem n, że pochodna w sensie dystrybucyjnym ![]() może być wyznaczona jako
może być wyznaczona jako
| (8.6) |
Najpierw obliczamy dla ![]() jak następuje
jak następuje
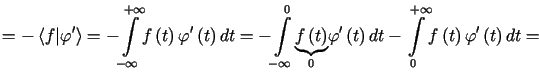 |
||
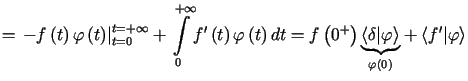 , , |
tzn. ![]() .
Stąd dalej łatwo przez indukcję uzyskać wzór (8.6)
dla dowolnego n. Stosując do wzoru (8.6)
twierdzenie o transformacie pochodnej (w sensie dystrybucyjnym) otrzymujemy
.
Stąd dalej łatwo przez indukcję uzyskać wzór (8.6)
dla dowolnego n. Stosując do wzoru (8.6)
twierdzenie o transformacie pochodnej (w sensie dystrybucyjnym) otrzymujemy
T w i e r d z e n i e (o różniczkowaniu transformaty)
Dla dowolnego ![]() prawdziwy jest wzór
prawdziwy jest wzór
Widać, że wystarczy przeprowadzić dowód w przypadku ![]() (dalej natychmiast przez indukcję). Niech
(dalej natychmiast przez indukcję). Niech ![]() .
Stąd
.
Stąd ![]() .
Ponieważ na mocy własności klasycznej transformaty Laplace'a
.
Ponieważ na mocy własności klasycznej transformaty Laplace'a ![]() ,
więc
,
więc
![$\displaystyle D^{k}\left[ \left( -t\right) h\left( t\right) \right] =-\binom{k}......dot D^{k-1}h\left( t\right)=-tD^{k}h\left( t\right) -kD^{k-1}h\left( t\right)$](img1202.gif)